
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Три способа решения задач про количество ног у двух видов животных
Методические материалы по теме:
На вступительных экзаменах в физматшколы и на математических олимпиадах часто можно встретить вот такого рода задачи:
В клетке сидят куры и кролики. У них в сумме 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?
Решать их можно тремя способами - арифметически по действиям, с помощью уравнений и с помощью системы уравнений. Среди педагогов ведутся дискуссии о том, как именно учить решать детей такого рода задачи и какое решение можно от них требовать.
С одной стороны, решить такую задачу с помощью уравнений просто, а с помощью системы уравнений ещё проще – и именно такого решения могут требовать на вступительных экзаменах. С другой стороны, противники такого метода говорят, что для развития логического мышления в 4-м классе полезней показать, как такую задачу можно решить без уравнений – т.к. решать уравнениями ребёнок неизбежно научится позже. И какие-то школы на вступительных экзаменах могут требовать решения задачи именно арифметически, а не через уравнения. Мы же покажем все три способа.
Итак, повторим условие задачи:
В клетке сидят куры и кролики. У них 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?
Способ 1. Арифметическое решение
В задаче две неизвестных – число куриц и число кроликов. Попробуем обойтись без введения неизвестных x и y и решим задачу путём логических рассуждений и простейших арифметических действий.
Предположим, что в клетке сидят только куры. У каждой курицы (как и у каждого кролика) только одна голова. Значит если по условию задачи мы имеем 40 голов в клетке, и в клетке только курицы, значит в клетке 40 куриц.
1) У каждой курицы по 2 ноги, значит у 40 куриц 80 ног: 40∙2 = 80.
2) Однако, по условию задачи, в клетке не 80 ног, а 124. Значит мы не учли 124-80 = 44 ноги.
Как мы знаем, у кроликов 4 ноги. При этом, предполагая, что в клетке только курицы, мы уже учли по две ноги каждого кролика (предполагая, что это куриные ноги). Остались неучтёнными по 2 других ноги каждого кролика.
Как мы уже вычислили выше, всего у нас 44 неучтённых ноги. Значит, раз на каждого кролика по 2 неучтённых ноги, то получается, что кроликов 44:2 = 22 штуки.
Итак, число кроликов мы узнали. Т.к. в сумме кур и кроликов 40, то число кур мы легко находим:
40 – 22 = 18
Всего в клетке 18 кур и 22 кролика.
Проверим наше решение, подсчитав общее число ног.
Число ног у кроликов:
22∙4 = 88
Число ног у кур:
18∙2 = 36
Общее число ног кур и кроликов: 88+36 = 124 – что соответствует условию задачи. Значит задача решена верно.
Ответ: 22 кролика, 18 куриц
Вроде бы в этой задачи достаточно простые рассуждения, но для учения 4-го класса они могут быть вовсе не очевидными. Если он знаком с решением уравнений, то для него значительно более простым может оказаться решение через уравнение.
Способ 2. Решение через уравнение
Введём обозначение:
x - число куриц
40 – x – число кроликов
Составим уравнение для числа ног, зная, что у куриц 2 ноги, а у кроликов 4
2x + 4(40-x) = 124
2x + 160 – 4x = 124
160 - 124 = 4x - 2x
36 = 2x
x = 18
Итак, число куриц: 18
Число кроликов: 40 – 18= 22
Ответ: 22 кролика, 18 куриц
Мы получили тот же ответ, что и в первом способе
Способ 3. Решение через систему уравнений
Введём обозначения:
x – число куриц
y – число кроликов
Составим систему уравнений:
2x + 4y = 124
Выразим x из первого уравнения
x = 40 – y
Подставим x во второе уравнение:
2(40 – y) + 4y = 124
80 – 2y + 4y = 124
2y = 44
y = 22
x = 40 – 22 = 18
Ответ: 22 кролика, 18 куриц
В клетке сидят куры и кролики. У них в сумме 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?
Решать их можно тремя способами - арифметически по действиям, с помощью уравнений и с помощью системы уравнений. Среди педагогов ведутся дискуссии о том, как именно учить решать детей такого рода задачи и какое решение можно от них требовать.
С одной стороны, решить такую задачу с помощью уравнений просто, а с помощью системы уравнений ещё проще – и именно такого решения могут требовать на вступительных экзаменах. С другой стороны, противники такого метода говорят, что для развития логического мышления в 4-м классе полезней показать, как такую задачу можно решить без уравнений – т.к. решать уравнениями ребёнок неизбежно научится позже. И какие-то школы на вступительных экзаменах могут требовать решения задачи именно арифметически, а не через уравнения. Мы же покажем все три способа.
Итак, повторим условие задачи:
В клетке сидят куры и кролики. У них 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Способ 1. Арифметическое решение
В задаче две неизвестных – число куриц и число кроликов. Попробуем обойтись без введения неизвестных x и y и решим задачу путём логических рассуждений и простейших арифметических действий.
Предположим, что в клетке сидят только куры. У каждой курицы (как и у каждого кролика) только одна голова. Значит если по условию задачи мы имеем 40 голов в клетке, и в клетке только курицы, значит в клетке 40 куриц.
1) У каждой курицы по 2 ноги, значит у 40 куриц 80 ног: 40∙2 = 80.
2) Однако, по условию задачи, в клетке не 80 ног, а 124. Значит мы не учли 124-80 = 44 ноги.
Как мы знаем, у кроликов 4 ноги. При этом, предполагая, что в клетке только курицы, мы уже учли по две ноги каждого кролика (предполагая, что это куриные ноги). Остались неучтёнными по 2 других ноги каждого кролика.
Как мы уже вычислили выше, всего у нас 44 неучтённых ноги. Значит, раз на каждого кролика по 2 неучтённых ноги, то получается, что кроликов 44:2 = 22 штуки.
Итак, число кроликов мы узнали. Т.к. в сумме кур и кроликов 40, то число кур мы легко находим:
40 – 22 = 18
Всего в клетке 18 кур и 22 кролика.
Проверим наше решение, подсчитав общее число ног.
Число ног у кроликов:
22∙4 = 88
Число ног у кур:
18∙2 = 36
Общее число ног кур и кроликов: 88+36 = 124 – что соответствует условию задачи. Значит задача решена верно.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Ответ: 22 кролика, 18 куриц
Вроде бы в этой задачи достаточно простые рассуждения, но для учения 4-го класса они могут быть вовсе не очевидными. Если он знаком с решением уравнений, то для него значительно более простым может оказаться решение через уравнение.
Способ 2. Решение через уравнение
Введём обозначение:
x - число куриц
40 – x – число кроликов
Составим уравнение для числа ног, зная, что у куриц 2 ноги, а у кроликов 4
2x + 4(40-x) = 124
2x + 160 – 4x = 124
160 - 124 = 4x - 2x
36 = 2x
x = 18
Итак, число куриц: 18
Число кроликов: 40 – 18= 22
Ответ: 22 кролика, 18 куриц
Мы получили тот же ответ, что и в первом способе
Способ 3. Решение через систему уравнений
Введём обозначения:
x – число куриц
y – число кроликов
Составим систему уравнений:
{
x + y = 402x + 4y = 124
Выразим x из первого уравнения
x = 40 – y
Подставим x во второе уравнение:
2(40 – y) + 4y = 124
80 – 2y + 4y = 124
2y = 44
y = 22
x = 40 – 22 = 18
Ответ: 22 кролика, 18 куриц
Дата публикации
Другие методические материалы по теме
Задачи раздела:

Из слитка меди сделали жетоны по 20 г каждый. При этом остались неизрасходованными 40 г меди. Если бы сделали столько же жетонов по 25 г, то не хватило бы 110 г меди. Какова масса слитка?

На трех складах было по одинаковому количеству ящиков с апельсинами. После того как со всех трех складов отправили 76 ящиков апельсинов, на первом складе осталось 73 ящика апельсинов, на втором - 81 ящик, на третьем - 70 ящиков. Сколько ящиков апельсинов отправили с каждого склада?
Велосипедист едет из города А в город Б со скоростью 15 км/ч. Если он будет ехать со скоростью 20 км/ч, то приедет на 3 часа раньше. Каково расстояние между городами?
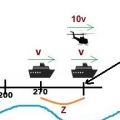
Океанский лайнер отправился в рейс. Когда он отошёл от берега на 270 км, за ним вылетел вертолёт с опоздавшим пассажиром. Скорость вертолёта в 10 раз больше скорости лайнера. На каком расстоянии от берега вертолёт догонит лайнер?

У Пети число почтовых марок в 3 раза больше, чем у Саши, и на 11 марок больше, чем у Оли. Всего у них в сумме 199 марок. Найдите число марок у Пети, Саши и Оли.

Площадь прямоугольного листа картона равна 50 см2 и ещё половину листа. Чему равна площадь листа?
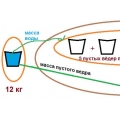
Ведро с водой весит 12 кг и масса пустого ведра в 5 раз меньше массы воды. Найдите массу пустого ведра и массу воды.

Примеры решения простейших уравнений в 4-5 классе.

Вводный урок по уравнениям. Что такое уравнения, для чего они нужны, основные методы решения уравнений.