
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Решение задач на нахождение периметра, площади, объёма фигур
Показываем, как в 4-5 классе решать задачи на нахождение периметра, площади и объёма фигур.
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
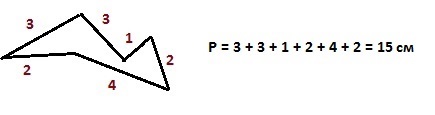
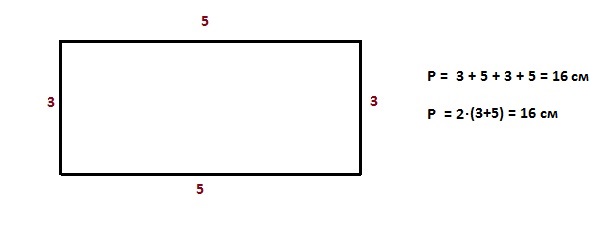
Периметр прямоугольника – удвоенная сумма длины и высоты - 2∙(a+b)
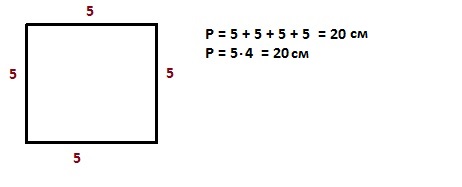
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
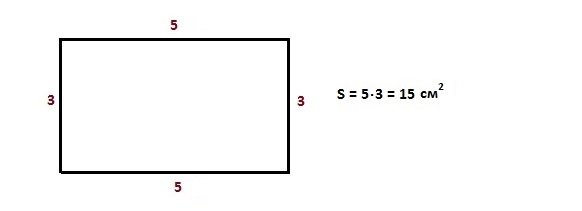
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Разделим этот прямоугольник на квадраты
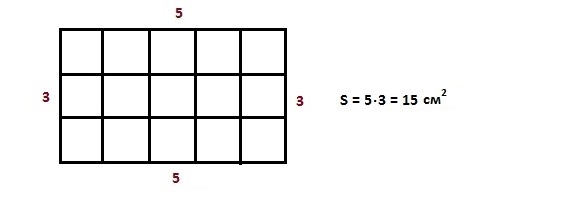
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
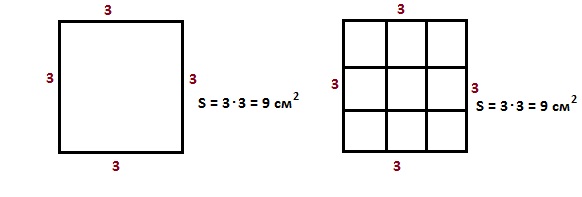
Площадь квадрата – произведение длины стороны на саму себя.
СОСТАВНЫЕ ФИГУРЫ
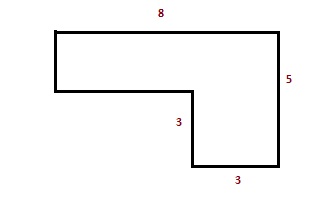
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
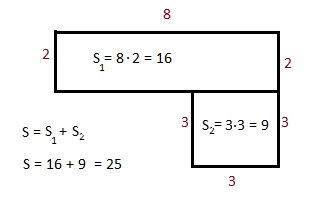
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
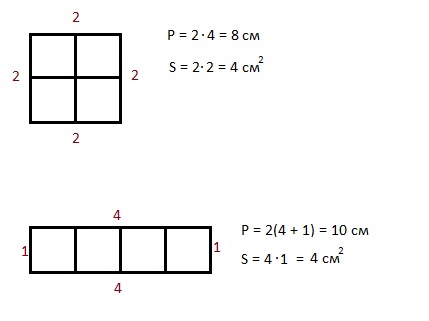
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты

Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
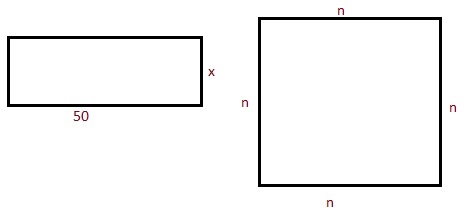
1. Вычислим сторону квадрата
4∙n = 80 - периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
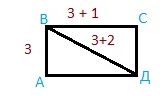
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
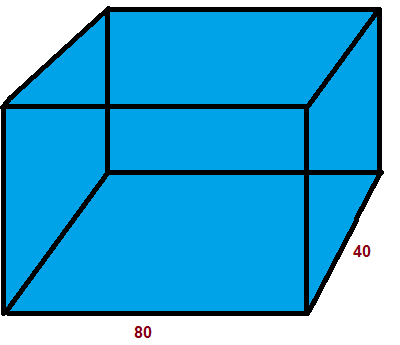
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см
Дата публикации
Задачи раздела:
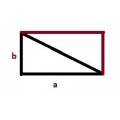
Площадь прямоугольного треугольника равна 32 см2. Подберите длины сторон, образующих прямой угол. Постарайтесь найти несколько решений.
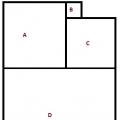
Фигуры A, B, C, D – квадраты. Периметр квадрата B равен 20 см, а периметр квадрата С равен 80 см. Чему равен периметр квадрата D.
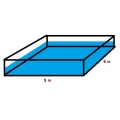
В прямоугольный надувной бассейн длиной 5 м и шириной 6 м вылили бочку с водой объёмом 240 л, которая была заполнена наполовину. Какой высоты будет уровень воды в бассейне? Напоминаем, что один литр воды равен одному кубическому дециметру.
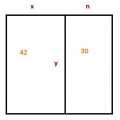
Квадрат разрезали на 2 прямоугольника. Периметр одного из них равен 42 см, второго 30 см. Найдите сторону квадрата.
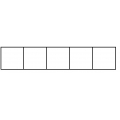
Прямоугольник разрезали на 5 одинаковых квадратов, сумма периметров которых 60 см. Найдите площадь исходного прямоугольника.
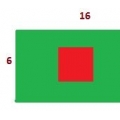
На прямоугольном листе бумаги длиной 16 см и шириной 6 см нарисован красный квадрат, периметр которого 12 см. Найдите площадь зелёной части листа.
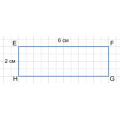
Даны два прямоугольника. Периметр первого на 10 см больше периметра второго, а ширина первого прямоугольника на 8 см меньше длины второго. На сколько сантиметров длина первого прямоугольника больше ширины второго прямоугольника?
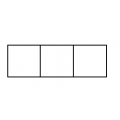
Из трёх одинаковых квадратов сложили прямоугольник. Чему равен периметр
прямоугольника, если периметр одного квадрата 22 см?
прямоугольника, если периметр одного квадрата 22 см?