Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Задача: Из деревни Окунево в деревню Карасево расстояние между которыми 17 км выехал велосипедист со скоростью 12 км/час. Одновременно с ним из Окунево в Карасево вышел пешеход со скоростью 5 км/час
Методические материалы по теме:
Условие задачи
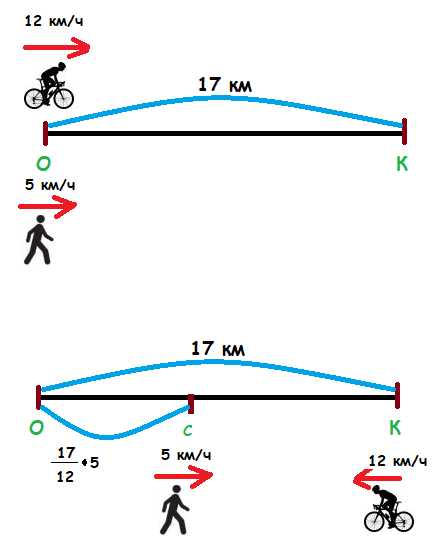
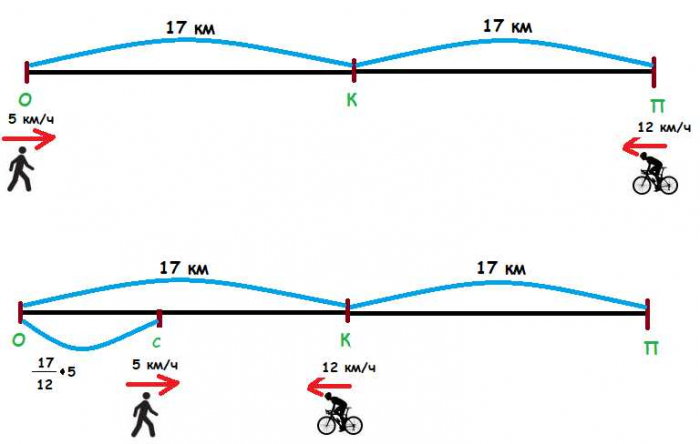
Из деревни Окунево в деревню Карасево расстояние между которыми 17 км выехал велосипедист со скоростью 12 км/час.
Одновременно с ним из Окунево в Карасево вышел пешеход со скоростью 5 км/час. Велосипедист доехал до Карасево и тотчас поехал обратно с той же скоростью.
Через сколько времени после начала движения они встретятся?
Раскрыть решение
Методические материалы по теме
Задачи раздела:

Мышке до норки 20 шагов. Кошке до мышки 5 прыжков. За один прыжок кошки мышка делает 3 шага. Один прыжок кошки равен 10 шагам мышки. Догонит ли кошка мышку?

Мыша и Коша одновременно стартовали на дистанцию 10 км. Трасса проходит по парку и состоит из 10 одинаковых кругов, по 1 км каждый. Мыша бежит в темпе 3 минуты на километр, а Коша не торопится, пробегает километр за 5 минут. Сколько раз на протяжении дистанции Мыша обгонял Кошу? Отрыв Мыши на старте не считается, обгон в момент финиша Мыши – считается.
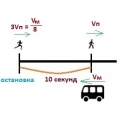
Коля, проезжая на маршрутке, заметил старого друга Петю, которого давно не видел. Петя шёл по тротуару в противоположную сторону. Через 10 секунд маршрутка подъехала к остановке и Коля, выйдя из неё, побежал догонять Петю. Через сколько секунд он его догонит, если Коля бежит в 3 раза быстрее, чем идет Петя и в 8 раз медленнее, чем едет маршрутка?
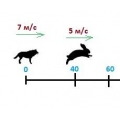
Волк бегает за зайцем по кругу длиной 60 метров. В начале погони расстояние между ними по часовой стрелке 40 метров и бегут они тоже по часовой стрелке. Скорость зайца - 5 м/с, скорость волка – 7 м/с. Но так как волк уже старенький, он может пробежать максимум два круга. Успеет ли волк поймать зайца?
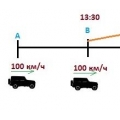
Автомобиль выехал из города А в город Б, а мотоцикл из Б в А. В 13:30 между ними было 200 км. В 16:30 между ними было 280 км. Найдите скорость мотоцикла, если скорость автомобиля 100 км/ч.
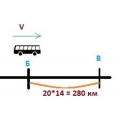
Автобус проходит путь от города А до города Б за 14 часов. Если бы скорость автобуса была на 20 км/ч больше, то он бы прошел тот же путь за 10 часов. Определите расстояние от А до Б и скорость автобуса.
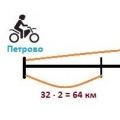
От деревни Петрово до деревни Ольгино 268 км. Ровно в 9 утра из Петрово в Ольгино выехал Вася на мопеде со скоростью 32 км/ч. Спустя два часа из Ольгино по той же дороге на мопеде выехал Петя со скоростью 19 км/ч навстречу Васе. Учитывая, что Вася и Петя движутся с постоянными скоростями без остановок, найдите: а) В какое время они встретятся? б) Какое расстояние проедет Вася до встречи с Петей?
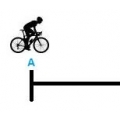
Велосипедист едет из города А в город Б со скоростью 15 км/ч. Если он будет ехать со скоростью 20 км/ч, то приедет на 3 часа раньше. Каково расстояние между городами?
Мотоциклист отправился из пункта М в пункт Н. Если его скорость будет 56 км/ч, то он опоздает на 2 часа. Если же он увеличит скорость с самого начала до 80 км/ч, то приедет раньше срока на 1 час. Найдите расстояние между пунктами М и Н и время, которое нужно потратить мотоциклисту, чтобы прибыть в пункт Н вовремя.

Два землекопа начали одновременно рыть канаву с двух концов навстречу друг другу. Первый землекоп рыл со скоростью 550 см/ч, а другой со скоростью 650 см/ч. Определите длину канавы, если она была вырыта за 3 часа 30 минут.

Путешественник вышел из дома в 8:30 и, пройдя 14 км за 3 часа, получил звонок из дома, который заставил его срочно вернуться. Обратно он побежал со скоростью в 4 раза быстрее, чем шёл из дома. Во сколько он прибежит домой?

Александр вышел из дома и пошёл со скоростью 40 м/мин. После того, как он прошёл 1200 м, за ним вдогонку вышел Пётр со скоростью 60 м/мин. Пётр взял с собой собаку, которая стала бегать между Петром и Александром со скоростью 130 м/мин до тех пор, пока они не встретились. Сколько всего метров она пробежала?
Путешественник шёл из пункта А в пункт Б со скоростью 6 км/ч, а обратно из Б в А, уставший, со скоростью 3 км/ч. Весь путь занял у него 12 часов.
Найдите расстояние, которое прошел путешественник.
Найдите расстояние, которое прошел путешественник.

Теплоход движется по реке с собственной скоростью 44 км/ч. Скорость течения реки – 50 м/мин. Какой путь пройдёт теплоход за 4 часа против течения реки?
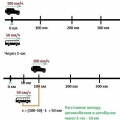
Основные формулы и методы решения задач на движение в 4 и 5 классе.