
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Основные принципы решения уравнений
Методические материалы по теме:
В этом уроке мы рассмотрим, что такое уравнения, для чего они нужны, основные методы решения уравнений в 4 и 5 классе.
Ранее вы могли проходить в школе такого рода примеры:
Как вы знаете, такие выражения называются уравнениями, а вместо кружка используется буква x или любая другая.
5 + x = 11 – это уравнение. Уравнением оно называется потому что в нём левая часть равняется правой. Если условие равенства не выполняется, значит уравнение записано неверно. Буква x называется неизвестным, или корнем уравнения. Целью решения уравнения является нахождение неизвестного.
Как вы уже знаете, для того, чтобы решить уравнение, надо x оставить в одной части, а все числа перенести в другую часть с противоположным знаком.
Правило:
То есть если у нас
5 + x =11
то
x = 11 – 5
x = 6
Другой пример:
y + 21 = 37
y = 37 - 21
y = 16
Обратите внимание, что я специально здесь использовал вместо x букву y – для того, чтобы подчеркнуть, что в уравнении неизвестное может обозначаться не только x, но и любой другой буквой или даже комбинацией букв.
Если же мы имеем уравнение вот такого вида:
26 – x = 18
то мы можем записать, что
26 – 18 = x – здесь, как вы видите, мы 18 перенесли в левую часть со знаком минус, а x – в правую со знаком плюс.
При этом мы можем поменять левую и правую часть местами, от этого суть уравнения не поменяется. То есть мы можем записать, что
x = 26 - 18
x = 8
Для проверки решения уравнения надо найденное неизвестное подставить в исходное уравнение. Т.е. в нашем случае это
26 – 8 = 18
18 = 18 – решение верное.
Пример:
z – 7 = 14
z = 14 + 7
z = 21
Проверка:
21 – 7 = 14
14 = 14 – решение верное
Запишем равенство
6 = 6
Если мы умножим обе части равенства на одно и то же число, то оно останется верным
6∙3 = 6∙3
Если мы разделим обе части равенства на одно и то же число, то оно тоже останется верным
6:2 = 6:2
5∙x = 15
Как уже говорилось ранее, мы можем разделить правую и левую часть на одно и то же число, и равенство сохранится. Чтобы найти x, это уравнение нужно разделить на 5.
Для того, чтобы разделить на 5 выражение 5∙x мы можем записать
5x:5
или
(5:5)x = 1∙x = x
Таким образом, из начального уравнения 5∙x = 15 получим:
5x:5 = 15:5
x = 3
Можно сказать по другому:
Здесь 5 и x – это множители, а 15 – произведение.
То есть x = 15:5 = 3
Проверка:
5∙3 = 15
15 = 15
Пример:
x∙4 = 32 (x∙4 – это то же самое, что 4∙x)
x = 32:4
x = 8
z:4 = 16
Здесь z – делимое, 4 – делитель, 16 – частное. Для того, чтобы найти делимое, надо частное умножить на делитель. Ещё раз обращаю ваше внимание, что неизвестное может обозначаться любой буквой, не обязательно только x.
z = 16∙4
z = 64
В правой части у нас остался один z, потому что ранее это был z в 4 раза меньший, и раз мы его умножили на 4, то он стал в 4 раза больше, т.е. полным z.
Проверка
64:4 = 16
16 = 16
Пример
120:x = 30
120 = 30∙x – мы умножили на x левую и правую часть, в результате чего в левой части он исчез, а в правой части он появился. Левая часть – это было число 120, уменьшенное в x раз (так как деление – это уменьшение числа в заданное число раз). Соответственно, раз мы левую часть умножаем на тот же x, то она перестаёт быть числом 120, уменьшенным в x раз, и станет просто числом 120.
Таким образом, мы перешли к уже известным нам уравнениям с множителями
Мы можем переписать равенство как
30∙x = 120
x = 120:30
x = 4
Про это же уравнение можно сказать следующее:
120:x = 30
120 – делимое, x – делитель, 30 - частное
Пример:
96:x = 6
96 = 6x
x = 96:6 – тут мы пропустили шаг перестановки частей равенства 6x = 96 – его записывать необязательно
x = 16
Пример:
3x + x = 24
4x = 24
x = 24:4
x = 6
Проверка:
3x + x = 24
3∙6 + 6 = 24
18 + 6 = 24
24 = 24
11x – 3x + 5x = 65
13x = 65
x = 65:13
x = 5
Проверка:
11∙5 – 3∙5 + 5∙5 = 65
55 – 15 + 25 = 65
65 = 65
Предположим, у нас есть выражение
9∙(10 - 4)
Мы можем записать его как
9∙6
так как выражение в скобках 10-4 равно 6. 9∙6 = 54
Или же мы можем раскрыть скобки.
Т.е
9∙(10 - 4) = 9∙10 – 9∙4 = 90 – 36 = 54
Аналогично, если в скобках будет больше членов и с разными знаками.
Например:
(11 + 2 – 5)∙4 = 4∙8 = 32
или
(11 + 2 – 5)∙4 = 4∙11 + 4∙2 – 4∙5 = 44 + 8 – 20 = 32 -
как мы уже говорили, множитель может стоять и после скобок, от этого правила раскрытия скобок не меняются.
Если в скобках вместо числа будет стоять неизвестное, то скобки раскрываются аналогично.
12∙(8x + 2x – 5) = 12∙8x + 12∙2x – 12∙5 = 96x + 24x – 60 = 120x - 60
Пример:
16∙(x – 4) = 4∙(x+2)
У правой части мы видим множитель 4. В левой части множитель 16. Т.е. мы смело можем разделить обе части на 4, избавишись таким образом от множителя в правой части
4∙(x – 4) = x +2
4x – 16 = x + 2
далее переносим x в левую часть, а числа – в правую
4x – x = 16+2
3x = 18
x = 6
Проверка:
16∙(6 – 4) = 4∙(6+2)
16∙2 = 4∙8
32 = 32
Пример:
5∙(15 – x) = 25∙(x-3)
Разделим обе части уравнения на 5
15 – x = 5∙(x-3)
15 – x = 5x – 15
15 + 15 = 5x + x
30 = 6x
x = 5
Проверка:
5∙(15 – 5) = 25∙(5 – 3)
5∙10 = 25∙2
50 = 50
Пример:
100:(x – 25) = 20
Точно так же, как мы решали ранее уравнение 120:x = 30 путём умножения обеих частей на делитель, т.е. на x, и получая 120 = 30x, это уравнение мы тоже решим, умножив обе части на делитель, т.е. на x-25
100 = 20(x-25)
100 = 20x – 500
100 + 500 = 20x
600 = 20x
x = 30
Проверка
100:(30-25) = 20
100:5 = 20
20 = 20
Пример
(x – 4):6 = 16
x – 4 = 16∙6
x – 4 = 96
x = 96+4
x = 100
Проверка:
(100-4):6 = 16
96:6 = 16
16 = 16
Простейшие уравнения
Ранее вы могли проходить в школе такого рода примеры:
Впишите в кружок подходящее число:
5+ ⃝ = 11
5+ ⃝ = 11
Как вы знаете, такие выражения называются уравнениями, а вместо кружка используется буква x или любая другая.
5 + x = 11 – это уравнение. Уравнением оно называется потому что в нём левая часть равняется правой. Если условие равенства не выполняется, значит уравнение записано неверно. Буква x называется неизвестным, или корнем уравнения. Целью решения уравнения является нахождение неизвестного.
Как вы уже знаете, для того, чтобы решить уравнение, надо x оставить в одной части, а все числа перенести в другую часть с противоположным знаком.
Правило:
Мы можем переносить числа и неизвестные из одной части равенства в другую, поменяв при этом знак на противоположный.
То есть если у нас
5 + x =11
то
x = 11 – 5
x = 6
Другой пример:
y + 21 = 37
y = 37 - 21
y = 16
Обратите внимание, что я специально здесь использовал вместо x букву y – для того, чтобы подчеркнуть, что в уравнении неизвестное может обозначаться не только x, но и любой другой буквой или даже комбинацией букв.
Если же мы имеем уравнение вот такого вида:
26 – x = 18
то мы можем записать, что
26 – 18 = x – здесь, как вы видите, мы 18 перенесли в левую часть со знаком минус, а x – в правую со знаком плюс.
При этом мы можем поменять левую и правую часть местами, от этого суть уравнения не поменяется. То есть мы можем записать, что
x = 26 - 18
x = 8
Для проверки решения уравнения надо найденное неизвестное подставить в исходное уравнение. Т.е. в нашем случае это
26 – 8 = 18
18 = 18 – решение верное.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Пример:
z – 7 = 14
z = 14 + 7
z = 21
Проверка:
21 – 7 = 14
14 = 14 – решение верное
Уравнения с делением и умножением
Запишем равенство
6 = 6
Если мы умножим обе части равенства на одно и то же число, то оно останется верным
6∙3 = 6∙3
Если мы разделим обе части равенства на одно и то же число, то оно тоже останется верным
6:2 = 6:2
Важно: эти принципы часто используются при решении уравнений
Уравнение c множителями
5∙x = 15
Как уже говорилось ранее, мы можем разделить правую и левую часть на одно и то же число, и равенство сохранится. Чтобы найти x, это уравнение нужно разделить на 5.
Для того, чтобы разделить на 5 выражение 5∙x мы можем записать
5x:5
или
(5:5)x = 1∙x = x
Таким образом, из начального уравнения 5∙x = 15 получим:
5x:5 = 15:5
x = 3
Можно сказать по другому:
Здесь 5 и x – это множители, а 15 – произведение.
Для того, чтобы найти неизвестный множитель, надо произведение разделить на другой множитель, который нам известен.
То есть x = 15:5 = 3
Проверка:
5∙3 = 15
15 = 15
Пример:
x∙4 = 32 (x∙4 – это то же самое, что 4∙x)
x = 32:4
x = 8
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Уравнение с делителями
z:4 = 16
Здесь z – делимое, 4 – делитель, 16 – частное. Для того, чтобы найти делимое, надо частное умножить на делитель. Ещё раз обращаю ваше внимание, что неизвестное может обозначаться любой буквой, не обязательно только x.
z = 16∙4
z = 64
В правой части у нас остался один z, потому что ранее это был z в 4 раза меньший, и раз мы его умножили на 4, то он стал в 4 раза больше, т.е. полным z.
Проверка
64:4 = 16
16 = 16
Пример
120:x = 30
120 = 30∙x – мы умножили на x левую и правую часть, в результате чего в левой части он исчез, а в правой части он появился. Левая часть – это было число 120, уменьшенное в x раз (так как деление – это уменьшение числа в заданное число раз). Соответственно, раз мы левую часть умножаем на тот же x, то она перестаёт быть числом 120, уменьшенным в x раз, и станет просто числом 120.
Таким образом, мы перешли к уже известным нам уравнениям с множителями
Мы можем переписать равенство как
30∙x = 120
x = 120:30
x = 4
Про это же уравнение можно сказать следующее:
Для того, чтобы найти неизвестный делитель x надо делимое разделить на частное.
120:x = 30
120 – делимое, x – делитель, 30 - частное
Пример:
96:x = 6
96 = 6x
x = 96:6 – тут мы пропустили шаг перестановки частей равенства 6x = 96 – его записывать необязательно
x = 16
Усложнённые уравнения
Неизвестные можно складывать и вычитать, как и числа
Пример:
3x + x = 24
4x = 24
x = 24:4
x = 6
Проверка:
3x + x = 24
3∙6 + 6 = 24
18 + 6 = 24
24 = 24
11x – 3x + 5x = 65
13x = 65
x = 65:13
x = 5
Проверка:
11∙5 – 3∙5 + 5∙5 = 65
55 – 15 + 25 = 65
65 = 65
Раскрытие скобок
Предположим, у нас есть выражение
9∙(10 - 4)
Мы можем записать его как
9∙6
так как выражение в скобках 10-4 равно 6. 9∙6 = 54
Или же мы можем раскрыть скобки.
При раскрытии скобок множитель, стоящий перед скобками (или после них), умножается на каждое число в скобках, при этом знаки сохраняются.
Т.е
9∙(10 - 4) = 9∙10 – 9∙4 = 90 – 36 = 54
Аналогично, если в скобках будет больше членов и с разными знаками.
Например:
(11 + 2 – 5)∙4 = 4∙8 = 32
или
(11 + 2 – 5)∙4 = 4∙11 + 4∙2 – 4∙5 = 44 + 8 – 20 = 32 -
как мы уже говорили, множитель может стоять и после скобок, от этого правила раскрытия скобок не меняются.
Если в скобках вместо числа будет стоять неизвестное, то скобки раскрываются аналогично.
12∙(8x + 2x – 5) = 12∙8x + 12∙2x – 12∙5 = 96x + 24x – 60 = 120x - 60
Пример:
16∙(x – 4) = 4∙(x+2)
У правой части мы видим множитель 4. В левой части множитель 16. Т.е. мы смело можем разделить обе части на 4, избавишись таким образом от множителя в правой части
4∙(x – 4) = x +2
4x – 16 = x + 2
далее переносим x в левую часть, а числа – в правую
4x – x = 16+2
3x = 18
x = 6
Проверка:
16∙(6 – 4) = 4∙(6+2)
16∙2 = 4∙8
32 = 32
Пример:
5∙(15 – x) = 25∙(x-3)
Разделим обе части уравнения на 5
15 – x = 5∙(x-3)
15 – x = 5x – 15
15 + 15 = 5x + x
30 = 6x
x = 5
Проверка:
5∙(15 – 5) = 25∙(5 – 3)
5∙10 = 25∙2
50 = 50
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример:
100:(x – 25) = 20
Точно так же, как мы решали ранее уравнение 120:x = 30 путём умножения обеих частей на делитель, т.е. на x, и получая 120 = 30x, это уравнение мы тоже решим, умножив обе части на делитель, т.е. на x-25
100 = 20(x-25)
100 = 20x – 500
100 + 500 = 20x
600 = 20x
x = 30
Проверка
100:(30-25) = 20
100:5 = 20
20 = 20
Пример
(x – 4):6 = 16
x – 4 = 16∙6
x – 4 = 96
x = 96+4
x = 100
Проверка:
(100-4):6 = 16
96:6 = 16
16 = 16
Дата публикации
Другие методические материалы по теме
Задачи раздела:

Из слитка меди сделали жетоны по 20 г каждый. При этом остались неизрасходованными 40 г меди. Если бы сделали столько же жетонов по 25 г, то не хватило бы 110 г меди. Какова масса слитка?

На трех складах было по одинаковому количеству ящиков с апельсинами. После того как со всех трех складов отправили 76 ящиков апельсинов, на первом складе осталось 73 ящика апельсинов, на втором - 81 ящик, на третьем - 70 ящиков. Сколько ящиков апельсинов отправили с каждого склада?

На вступительных экзаменах в физматшколы и на математических олимпиадах часто можно встретить вот такого рода задачи: "В клетке сидят куры и кролики. У них в сумме 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?"
Велосипедист едет из города А в город Б со скоростью 15 км/ч. Если он будет ехать со скоростью 20 км/ч, то приедет на 3 часа раньше. Каково расстояние между городами?
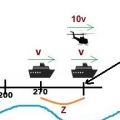
Океанский лайнер отправился в рейс. Когда он отошёл от берега на 270 км, за ним вылетел вертолёт с опоздавшим пассажиром. Скорость вертолёта в 10 раз больше скорости лайнера. На каком расстоянии от берега вертолёт догонит лайнер?

У Пети число почтовых марок в 3 раза больше, чем у Саши, и на 11 марок больше, чем у Оли. Всего у них в сумме 199 марок. Найдите число марок у Пети, Саши и Оли.

Площадь прямоугольного листа картона равна 50 см2 и ещё половину листа. Чему равна площадь листа?
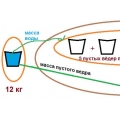
Ведро с водой весит 12 кг и масса пустого ведра в 5 раз меньше массы воды. Найдите массу пустого ведра и массу воды.

Примеры решения простейших уравнений в 4-5 классе.