
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Системы уравнений
Методические материалы по теме:
Рассказываем, как решать системы уравнений.
Рассмотрим уравнение с двумя неизвестными:
x + y = 10
У этого уравнения может быть много решений: x=1, y=9; x=2, y=8; x=3, y=7 и т.д.
Какое из решений выбрать - непонятно. Ситуация становится более определённой, если мы знаем, что между x и y существует ещё какая-то другая взаимосвязь. Например, мы знаем про те же самые x и y, что y-x = 2.
Итак, мы можем записать:
y - x = 2
То, что мы записали, называется системой уравнений. Уравнения, входящие в систему, объединяются большой фигурной скобкой. Чтобы система уравнений имела решение, число уравнений должно быть равно числу неизвестных.
Так как это связанные между собой уравнения, то мы можем выразить, например, y через x в первом уравнений, и подставить получившееся выражение вместо y во второе уравнение - тем самым во втором уравнении останется только одно неизвестное (x) и мы сможем решить уравнение.
Запишем это в виде формул.
x + y = 10
y = 10 - x
Подставляем полученное выражение 10 - x вместо y во второе уравнение:
y - x = 2
10 - x - x = 2
10 - 2 = x + x
8 = 2x
x = 4
Мы нашли x. Теперь найдём y, зная, что y = 10 - x
y = 10 - 4 = 6
Мы нашли x и y. x = 4, y = 6
Проверим наше решение, подставим x и y в оба уравнения системы:
x + y = 10
y - x = 2
4 + 6 = 10
6 - 4 = 2
10 = 10
2 = 2
В обеих уравнениях левые и правые части равны, то есть x и y мы нашли правильно.
Существует и другой метод решения уравнений
Рассмотрим систему уравнений:
2x + 3y = 35
Глядя на эту систему уравнений мы понимаем, что мы не можем выразить x или y через целые числа - 80 делится на цело на 5, но не делится нацело на 6, а 35 не делится нацело ни на 2, ни на 3. Если мы не умеем работать с дробными числами, то уравнение мы можем решить по другому.
Для решения этого уравнения надо из левой части первого уравнения вычесть левую часть второго уравнения, а из правой части первого вычесть правую часть второго. При этом не принципиально вычитать именно из первого уравнения второе - можно и из второго первое. Но если мы в данной системе уравнений вычтем из правой части второго уравнения правую часть
первого уравнения, то у нас получится 35 - 80 = -45, отрицательное число. Если с отрицательными числами мы работать ещё не умеем, то у нас остаётся только один вариант - из первого уравнения вычитать второе.
Итак, запишем соответствующую операцию вычитания частей уравнений в виде формулы:
5x + 6y - (2x + 3y) = 80 - 35
5x + 6y - 2x - 3y = 45
3x + 3y = 45
x + y = 15
Итак, мы получили простое уравнение x + y = 15, где отсутствуют множители у x и y.
Теперь мы можем выразить x через y (или y через x - это без разницы) и подставить получившееся выражение в одно из уравнений системы.
x = 15 - y
Подставим это выражение вместо x во второе уравнение
2x + 3y = 35
2(15 - y) + 3y = 35
30 - 2y + 3y = 35
y = 35 - 30
y = 5
Мы нашли y, осталось найти x
x = 15 - y
x = 15 - 5 = 10
Наш ответ: x = 10, y = 5
Проверим наше решение, подставив найденные x и y в систему уравнений:
2x + 3y = 35
5∙10 + 6∙5 = 80
2∙10 + 3∙5 = 35
50 + 30 = 80
20 + 15 = 35
80 = 80
35 = 35
Обе части в обеих уравнениях равны друг другу, значит наше решение верное.
Ответ: x = 10, y = 5
Уравнения можно не только вычитать друг из друга, но и складывать.
Например:
2x + 4y = 48
Если мы просуммируем оба уравнения, то у нас в правой части у неизвестных x и y будут одинаковые коэффициенты 7 - нам будет удобно на эту 7 поделить, чтобы оставить x и y без коэффициентов.
Сложим два уравнения:
5x + 3y + 2x + 4y = 48 + 71
7x + 7y = 119
x + y = 17
x = 17 - y
Подставим x во второе уравнение:
2x + 4y = 48
Сначала разделим обе части уравнения на 2
x + 2y = 24
Подставим x:
17 - y + 2y = 24
y = 24 - 17
y = 7
x = 17 - y
x = 17 - 7 = 10
Ответ: x = 10, y = 7
Пример 1
3n – m = 12
Выразим m через n во втором уравнении:
3n – m = 12
3n – 12 = m
m = 3n – 12
Подставим 3n – 12 вместо m в первое уравнение
2n + 3m = 19
2n + 3(3n – 12) = 19
2n + 9n – 36 = 19
11n = 55
n = 5
Мы нашли n, теперь найдём m
m = 3n – 12
m = 3∙5 – 12
m = 3
Проверка решения:
2∙5 + 3∙3 = 19
3∙5 – 3 = 12
Ответ: m=3, n = 5
Пример 2
13x + 6y = 142
2x – 4y = 12
x – 2y = 6
x = 6 + 2y
13x + 6y = 142
13(6 + 2y) + 6y = 142
78 + 26y + 6y = 142
32y = 64
y = 2
x = 6 + 2y
x = 6 + 2∙2 = 10
Проверка:
2∙10 – 4∙2 = 12
13∙10 + 6∙2 = 142
Ответ: x = 10, y = 2
Пример 3
8x – 2y = 34
8x – 2y = 34
Разделим левую и правую части уравнения на 2:
4x – y = 17
4x – 17 = y
Теперь в первое уравнение вместо y подставим 4x-17:
2x + 3y = 117
2x + 3(4x – 17) = 117
2x + 12x – 51 = 117
14x = 117+51
14x = 168
x = 12
y = 4x – 17
y = 4∙12 – 17
y = 31
Ответ: x = 12, y = 31
Пример 4
3x – 2y + 3z = 69
4z + y – x = 97
Мы имеем дело с системой уравнений, где три уравнения и три неизвестных.
Нас это не должно пугать. Для начала выразим одну неизвестную через две других, например, x через z и y. Так как в третьем уравнении у нас возле x нет никакого множителя, то именно через третье уравнение мы и будем выражать x.
4z + y – x = 97
4z + y – 97 = x
x = 4z + y – 97
Теперь подставим полученное выражение для x во второе уравнение.
3x – 2y + 3z = 69
3(4z + y – 97) – 2y + 3z = 69
12z + 3y – 291 – 2y + 3z = 69
15z + y = 360
y = 360 - 15z
Ранее мы выразили x через z и y:
x = 4z + y – 97
Теперь полученное выражение для y (y = 360 - 15z) подставим в это выражение для x
x = 4z + 360 – 15z – 97
x + 15z – 4z = 263
x + 11z = 263
x = 263 – 11z
Итак, теперь у нас есть x, выраженный через z, и y, выраженный через z.
Запишем эти выражение ещё раз:
x = 263 – 11z
y = 360 – 15z
Теперь мы можем эти выражения подставить в первое уравнение системы, и у нас получится уравнение с одним неизвестным - z
2x + 3y – 2z = 19
2(263 – 11z) + 3(360 – 15z) - 2z = 19
526 – 22z + 1080 – 45z – 2z = 19
526 + 1080 – 19 = 2z + 45z + 22z
1587 = 69z
z = 23
Теперь подставим z в выражения для x и y:
x = 263 – 11z = 263 – 11∙23 = 10
y = 360 – 15z = 360 – 15∙23 = 15
x = 10
y = 15
z = 23
Проверка:
2∙10 + 3∙15 – 2∙23 = 19
3∙10 – 2∙15 + 3∙23 = 69
4∙23 + 15 – 10 = 97
Ответ: x = 10, y = 15, z = 23
Пример 5
3x – 2y + 3z = 11
2x + 8y – 6z = 30
Эта система уравнений отличается от предыдущих тем, что в первом уравнении тут не три
неизвестных, а два. Но нас это не должно пугать - наоборот, нам это только упрощает задачу.
Выразим z через x в первом уравнении:
5x – z = 17
5x – 17 = z
z = 5x – 17
Подставим полученное выражение для z во второе уравнение.
3x – 2y + 3z = 11
3x – 2y + 3(5x – 17) = 11
3x – 2y + 15x – 51 = 11
18x – 2y = 62
9x – y = 31
9x – 31 = y
y = 9x – 31
Итак, теперь у нас есть z и y, выраженные через x. Запишем их ещё раз:
z = 5x – 17
y = 9x – 31
Теперь подставим эти выражения в третье уравнение
2x + 8y – 6z = 30
2x + 8(9x – 31) – 6(5x – 17) = 30
2x + 72x – 248 – 30x + 102 = 30
44x = 30 + 248 – 102
44x = 176
x = 4
Мы нашли x, теперь найдём z и y
z = 5x - 17
z = 5∙4 – 17 = 3
y = 9x – 31
y = 9∙4 – 31 = 5
x = 4
y = 5
z = 3
Проверка:
2∙4 + 8∙5 – 6∙3 = 30
3∙4 – 2∙5 + 3∙3 = 11
5∙4 – 3 = 17
Ответ: x = 4, y = 5, z = 3
Пример 6
4x + 5y = 75
Тут мы не можем выразить ни x, ни y, т.к. левая и правая части уравнений не делятся на цело и на 3, и на 4, ни на 5.
Поэтому воспользуемся описанным ранее способом - вычитанием частей уравнений друг из друга. Вычтем из второго уравнения первое:
4x + 5y – (4x + 3y) = 75 – 61
4x + 5y – 4x – 3y = 14
2y = 14
y = 7
Найденный y подставим в первое уравнение:
4x + 3∙7 = 61
4x + 21 = 61
4x = 40
x = 10
x = 10
y = 7
Проверка:
4∙10 + 3∙7 = 61
4∙10 + 5∙7 = 75
40 + 21 = 61
40 + 35 = 75
Ответ: x = 10, y = 7
Пример 7
3x + 7y = 71
Эту систему уравнений можно решить двумя способами.
Первый способ
Вычтем из второго уравнение первое.
3x + 7y – (2x + 5y) = 71 – 50
3x + 7y – 2x – 5y = 21
x + 2y = 21
x = 21 – 2y
Подставим выражение для x в первое уравнение.
2(21 – 2y) + 5y = 50
42 – 4y + 5y = 50
y = 8
Подставим найденный y в выражение для x
x = 21 – 2y
x = 21 – 2∙8 = 21 – 16 = 5
Проверка:
2∙5 + 5∙8 = 50
3∙5 + 7∙8 = 71
10 + 40 = 50
15 + 56 = 71
Второй способ
3x + 7y = 71
Умножим обе части первого уравнения на 3, а обе части второго уравнения на 2.
Тем самым мы в обеих уравнениях получим множитель 6 у x, после чего при вычитании одного
уравнения из другого x у нас уйдёт (6x - 6x = 0), и останется только y.
3(2x + 5y) = 3∙50
2(3x + 7y) = 2∙71
6x + 15y = 150
6x + 14y = 142
Вычтем из первого уравнения второе.
6x + 15y – (6x + 14y) = 150 – 142
6x + 15y – 6x – 14y = 8
y = 8
Подставим найденный y в первое уравнение системы:
2x + 5y = 50
2x + 5∙8 = 50
2x + 40 = 50
2x = 50 – 40
2x = 10
x = 5
Ответ: x = 5, y = 8
x + y = 10
У этого уравнения может быть много решений: x=1, y=9; x=2, y=8; x=3, y=7 и т.д.
Какое из решений выбрать - непонятно. Ситуация становится более определённой, если мы знаем, что между x и y существует ещё какая-то другая взаимосвязь. Например, мы знаем про те же самые x и y, что y-x = 2.
Итак, мы можем записать:
{
x + y = 10y - x = 2
То, что мы записали, называется системой уравнений. Уравнения, входящие в систему, объединяются большой фигурной скобкой. Чтобы система уравнений имела решение, число уравнений должно быть равно числу неизвестных.
Так как это связанные между собой уравнения, то мы можем выразить, например, y через x в первом уравнений, и подставить получившееся выражение вместо y во второе уравнение - тем самым во втором уравнении останется только одно неизвестное (x) и мы сможем решить уравнение.
Запишем это в виде формул.
x + y = 10
y = 10 - x
Подставляем полученное выражение 10 - x вместо y во второе уравнение:
y - x = 2
10 - x - x = 2
10 - 2 = x + x
8 = 2x
x = 4
Мы нашли x. Теперь найдём y, зная, что y = 10 - x
y = 10 - 4 = 6
Мы нашли x и y. x = 4, y = 6
Проверим наше решение, подставим x и y в оба уравнения системы:
x + y = 10
y - x = 2
4 + 6 = 10
6 - 4 = 2
10 = 10
2 = 2
В обеих уравнениях левые и правые части равны, то есть x и y мы нашли правильно.
Почему мы смогли воспользоваться этим приёмом - выразить y через x в первом уравнении и подставить получившееся выражение вместо y во второе? Потому что у нас система уравнений и в этих двух уравнениях эти x и y - это одни и те же неизвестные, поэтому мы можем в одном уравнении заменять на выражения, полученные в другом
Не имеет значения - будем ли мы y выражать через x в первом уравнении и подставлять во второе, или во втором и подставлять в первое. Точно также не имеет значение, что именно мы будем подставлять - y, выраженный через x, или x, выраженные через y. Мы выражаем и подставляем то, что нам удобнее в дальнейших расчётах.
Существует и другой метод решения уравнений
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Вычитание одного уравнения из другого
Рассмотрим систему уравнений:
{
5x + 6y = 802x + 3y = 35
Глядя на эту систему уравнений мы понимаем, что мы не можем выразить x или y через целые числа - 80 делится на цело на 5, но не делится нацело на 6, а 35 не делится нацело ни на 2, ни на 3. Если мы не умеем работать с дробными числами, то уравнение мы можем решить по другому.
Для решения этого уравнения надо из левой части первого уравнения вычесть левую часть второго уравнения, а из правой части первого вычесть правую часть второго. При этом не принципиально вычитать именно из первого уравнения второе - можно и из второго первое. Но если мы в данной системе уравнений вычтем из правой части второго уравнения правую часть
первого уравнения, то у нас получится 35 - 80 = -45, отрицательное число. Если с отрицательными числами мы работать ещё не умеем, то у нас остаётся только один вариант - из первого уравнения вычитать второе.
Почему мы можем вычесть из из левой части одного уравнения левую часть другого, а из правой части одного правую часть другого и при этом быть уверенными, что равенство сохранится? Потому что это свойство систем уравнений. При вычитании соответствующих частей уравнений друг из друга, равенство сохраняется.
Итак, запишем соответствующую операцию вычитания частей уравнений в виде формулы:
5x + 6y - (2x + 3y) = 80 - 35
5x + 6y - 2x - 3y = 45
3x + 3y = 45
x + y = 15
Итак, мы получили простое уравнение x + y = 15, где отсутствуют множители у x и y.
Теперь мы можем выразить x через y (или y через x - это без разницы) и подставить получившееся выражение в одно из уравнений системы.
x = 15 - y
Подставим это выражение вместо x во второе уравнение
2x + 3y = 35
2(15 - y) + 3y = 35
30 - 2y + 3y = 35
y = 35 - 30
y = 5
Мы нашли y, осталось найти x
x = 15 - y
x = 15 - 5 = 10
Наш ответ: x = 10, y = 5
Проверим наше решение, подставив найденные x и y в систему уравнений:
{
5x + 6y = 802x + 3y = 35
5∙10 + 6∙5 = 80
2∙10 + 3∙5 = 35
50 + 30 = 80
20 + 15 = 35
80 = 80
35 = 35
Обе части в обеих уравнениях равны друг другу, значит наше решение верное.
Ответ: x = 10, y = 5
Сложение одного уравнения с другим
Уравнения можно не только вычитать друг из друга, но и складывать.
Например:
{
5x + 3y = 712x + 4y = 48
Если мы просуммируем оба уравнения, то у нас в правой части у неизвестных x и y будут одинаковые коэффициенты 7 - нам будет удобно на эту 7 поделить, чтобы оставить x и y без коэффициентов.
Сложим два уравнения:
5x + 3y + 2x + 4y = 48 + 71
7x + 7y = 119
x + y = 17
x = 17 - y
Подставим x во второе уравнение:
2x + 4y = 48
Сначала разделим обе части уравнения на 2
x + 2y = 24
Подставим x:
17 - y + 2y = 24
y = 24 - 17
y = 7
x = 17 - y
x = 17 - 7 = 10
Ответ: x = 10, y = 7
Пример 1
{
2n + 3m = 193n – m = 12
Выразим m через n во втором уравнении:
3n – m = 12
3n – 12 = m
m = 3n – 12
Подставим 3n – 12 вместо m в первое уравнение
2n + 3m = 19
2n + 3(3n – 12) = 19
2n + 9n – 36 = 19
11n = 55
n = 5
Мы нашли n, теперь найдём m
m = 3n – 12
m = 3∙5 – 12
m = 3
Проверка решения:
2∙5 + 3∙3 = 19
3∙5 – 3 = 12
Ответ: m=3, n = 5
Пример 2
{
2x – 4y = 12 13x + 6y = 142
2x – 4y = 12
x – 2y = 6
x = 6 + 2y
13x + 6y = 142
13(6 + 2y) + 6y = 142
78 + 26y + 6y = 142
32y = 64
y = 2
x = 6 + 2y
x = 6 + 2∙2 = 10
Проверка:
2∙10 – 4∙2 = 12
13∙10 + 6∙2 = 142
Ответ: x = 10, y = 2
Пример 3
{
2x + 3y = 1178x – 2y = 34
8x – 2y = 34
Разделим левую и правую части уравнения на 2:
4x – y = 17
4x – 17 = y
Теперь в первое уравнение вместо y подставим 4x-17:
2x + 3y = 117
2x + 3(4x – 17) = 117
2x + 12x – 51 = 117
14x = 117+51
14x = 168
x = 12
y = 4x – 17
y = 4∙12 – 17
y = 31
Ответ: x = 12, y = 31
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
{
2x + 3y – 2z = 193x – 2y + 3z = 69
4z + y – x = 97
Мы имеем дело с системой уравнений, где три уравнения и три неизвестных.
Нас это не должно пугать. Для начала выразим одну неизвестную через две других, например, x через z и y. Так как в третьем уравнении у нас возле x нет никакого множителя, то именно через третье уравнение мы и будем выражать x.
4z + y – x = 97
4z + y – 97 = x
x = 4z + y – 97
Теперь подставим полученное выражение для x во второе уравнение.
3x – 2y + 3z = 69
3(4z + y – 97) – 2y + 3z = 69
12z + 3y – 291 – 2y + 3z = 69
15z + y = 360
y = 360 - 15z
Ранее мы выразили x через z и y:
x = 4z + y – 97
Теперь полученное выражение для y (y = 360 - 15z) подставим в это выражение для x
x = 4z + 360 – 15z – 97
x + 15z – 4z = 263
x + 11z = 263
x = 263 – 11z
Итак, теперь у нас есть x, выраженный через z, и y, выраженный через z.
Запишем эти выражение ещё раз:
x = 263 – 11z
y = 360 – 15z
Теперь мы можем эти выражения подставить в первое уравнение системы, и у нас получится уравнение с одним неизвестным - z
2x + 3y – 2z = 19
2(263 – 11z) + 3(360 – 15z) - 2z = 19
526 – 22z + 1080 – 45z – 2z = 19
526 + 1080 – 19 = 2z + 45z + 22z
1587 = 69z
z = 23
Теперь подставим z в выражения для x и y:
x = 263 – 11z = 263 – 11∙23 = 10
y = 360 – 15z = 360 – 15∙23 = 15
x = 10
y = 15
z = 23
Проверка:
2∙10 + 3∙15 – 2∙23 = 19
3∙10 – 2∙15 + 3∙23 = 69
4∙23 + 15 – 10 = 97
Ответ: x = 10, y = 15, z = 23
Пример 5
{
5x - z = 173x – 2y + 3z = 11
2x + 8y – 6z = 30
Эта система уравнений отличается от предыдущих тем, что в первом уравнении тут не три
неизвестных, а два. Но нас это не должно пугать - наоборот, нам это только упрощает задачу.
Выразим z через x в первом уравнении:
5x – z = 17
5x – 17 = z
z = 5x – 17
Подставим полученное выражение для z во второе уравнение.
3x – 2y + 3z = 11
3x – 2y + 3(5x – 17) = 11
3x – 2y + 15x – 51 = 11
18x – 2y = 62
9x – y = 31
9x – 31 = y
y = 9x – 31
Итак, теперь у нас есть z и y, выраженные через x. Запишем их ещё раз:
z = 5x – 17
y = 9x – 31
Теперь подставим эти выражения в третье уравнение
2x + 8y – 6z = 30
2x + 8(9x – 31) – 6(5x – 17) = 30
2x + 72x – 248 – 30x + 102 = 30
44x = 30 + 248 – 102
44x = 176
x = 4
Мы нашли x, теперь найдём z и y
z = 5x - 17
z = 5∙4 – 17 = 3
y = 9x – 31
y = 9∙4 – 31 = 5
x = 4
y = 5
z = 3
Проверка:
2∙4 + 8∙5 – 6∙3 = 30
3∙4 – 2∙5 + 3∙3 = 11
5∙4 – 3 = 17
Ответ: x = 4, y = 5, z = 3
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 6
{
4x + 3y = 614x + 5y = 75
Тут мы не можем выразить ни x, ни y, т.к. левая и правая части уравнений не делятся на цело и на 3, и на 4, ни на 5.
Поэтому воспользуемся описанным ранее способом - вычитанием частей уравнений друг из друга. Вычтем из второго уравнения первое:
4x + 5y – (4x + 3y) = 75 – 61
4x + 5y – 4x – 3y = 14
2y = 14
y = 7
Найденный y подставим в первое уравнение:
4x + 3∙7 = 61
4x + 21 = 61
4x = 40
x = 10
x = 10
y = 7
Проверка:
4∙10 + 3∙7 = 61
4∙10 + 5∙7 = 75
40 + 21 = 61
40 + 35 = 75
Ответ: x = 10, y = 7
Пример 7
{
2x + 5y = 503x + 7y = 71
Эту систему уравнений можно решить двумя способами.
Первый способ
Вычтем из второго уравнение первое.
3x + 7y – (2x + 5y) = 71 – 50
3x + 7y – 2x – 5y = 21
x + 2y = 21
x = 21 – 2y
Подставим выражение для x в первое уравнение.
2(21 – 2y) + 5y = 50
42 – 4y + 5y = 50
y = 8
Подставим найденный y в выражение для x
x = 21 – 2y
x = 21 – 2∙8 = 21 – 16 = 5
Проверка:
2∙5 + 5∙8 = 50
3∙5 + 7∙8 = 71
10 + 40 = 50
15 + 56 = 71
Второй способ
{
2x + 5y = 503x + 7y = 71
Умножим обе части первого уравнения на 3, а обе части второго уравнения на 2.
Тем самым мы в обеих уравнениях получим множитель 6 у x, после чего при вычитании одного
уравнения из другого x у нас уйдёт (6x - 6x = 0), и останется только y.
3(2x + 5y) = 3∙50
2(3x + 7y) = 2∙71
6x + 15y = 150
6x + 14y = 142
Вычтем из первого уравнения второе.
6x + 15y – (6x + 14y) = 150 – 142
6x + 15y – 6x – 14y = 8
y = 8
Подставим найденный y в первое уравнение системы:
2x + 5y = 50
2x + 5∙8 = 50
2x + 40 = 50
2x = 50 – 40
2x = 10
x = 5
В этой системе уравнений мы применили такой приём, как умножение обеих уравнений на разные числа так, чтобы у одного из неизвестных (в нашем случае у x) в обеих уравнениях оказался один и тот же множитель. После этого мы вычли одно уравнение из другого, x у нас исчез, и мы легко смогли найти y.
Ответ: x = 5, y = 8
Дата публикации
Другие методические материалы по теме
Задачи раздела:

На вступительных экзаменах в физматшколы и на математических олимпиадах часто можно встретить вот такого рода задачи: "В клетке сидят куры и кролики. У них в сумме 40 голов и 124 ноги. Сколько кур и сколько кроликов в клетке?"
Два друга несли кирпичи. Один из друзей пожаловался, что ему тяжело их нести и предложил один из кирпичей, которые он нёс, взять его другу. Тот ему ответил – «Если я возьму у тебя кирпич, то их у меня станет в два раза больше, чем у тебя, а вот если ты у меня заберёшь кирпич, то у нас их станет поровну».
Сколько кирпичей нёс каждый из друзей?
Сколько кирпичей нёс каждый из друзей?

На ферме имеются курицы и овцы общим числом 42, а общее количество ног у них равно 134. Сколько на ферме овец?

1 ручка стоит как два карандаша, а одна ручка и 6 карандашей стоят 160 руб. Сколько стоят ручка и карандаш?
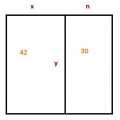
Квадрат разрезали на 2 прямоугольника. Периметр одного из них равен 42 см, второго 30 см. Найдите сторону квадрата.