
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Задачи на переливание из одного сосуда в другой
Методические материалы по теме:
Рассказываем, как в 4-5 классе решать задачи на переливание из одного сосуда в другой.
Задачи на переливание заключаются в том, что даётся два (иногда больше) сосудов разного объема, и путём манипуляций с наливанием воды в сосуды и переливанием из одного сосуда в другой надо добиться, чтобы в одном из сосудов оказался ровно заданный объём воды. Меток, указывающий объём, на сосудах нет, "на глазок" наливать нельзя.
Самый простой пример - пусть у нас есть два сосуда - 5 и 7 литров. Надо в один из сосудов налить ровно три литра воды.
Шаг 1. Наливаем в сосуд 5 л воды до краёв. Тем самым мы получаем 5 литров воды.
Шаг 2. Переливаем эту воду в сосуд 7 л. Теперь в нём 5 литров, а сосуд 5 литров пустой.
Шаг 3. Опять наливаем в сосуд 5 л. воду. В сосуде 7 л сейчас налито 5 л воды, значит есть ещё место для двух литров.
Шаг 4. Переливаем воду из сосуда 5 л в сосуд 7 л, пока он не наполнится до краёв. Те самым мы нальём в него ровно 2 л, т.к. в нём уже было 5 л, и оставалось ещё место для 2 л воды.
Раз мы из сосуда 5 л отлили 2 л, то в нём осталось 3 л. Задача решена.
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов получить 1 л воды?
Изобразим решение на схеме. Прямоугольники означают сосуды, синий цвет - воду в сосудах. Под прямоугольниками - объём сосуда, над прямоугольником - объём воды в нём.
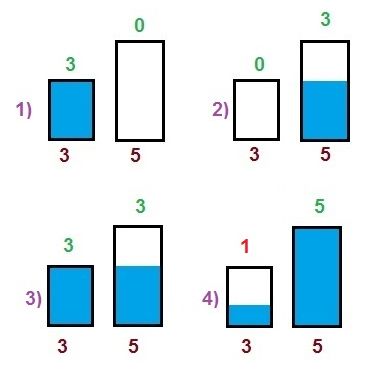
Пояснение к решению.
1 л воды можно получить, если из трёхлитрового сосуда отлить 2 литра воды. Значит нам надо добиться такой ситуации, когда в пятилитровом будем 3 литра воды, тем самым останется место ровно для двух литров, которые мы сможем перелить из трёхлитрового сосуда.
Шаг 1. Наливаем с трёхлитровый сосуд воду до краёв, получаем 3 литра воды
Шаг 2. Переливаем эту воду в пятилитровый сосуд. Теперь в нём 3 л воды, а в трёхлитровом пусто
Шаг 3. Опять наливаем в трёхлитровый сосуд воду, теперь по 3 л воды в каждом из сосудов.
Теперь мы добились той ситуации, которая нам была нужна - в пятилитровом сосуде есть место ровно для 2 л воды, а в трёхлитровом - 3 л воды.
Шаг 4. Переливаем воду из сосуда 3 л в сосуд 5 л, пока он не заполнится до краёв. Т.к. в нём было место для 2 л воды, то ровно эти 2 л и перельются, и в сосуде 3 л останется ровно 1 л. Залача решена.
Самый простой пример - пусть у нас есть два сосуда - 5 и 7 литров. Надо в один из сосудов налить ровно три литра воды.
Шаг 1. Наливаем в сосуд 5 л воды до краёв. Тем самым мы получаем 5 литров воды.
Шаг 2. Переливаем эту воду в сосуд 7 л. Теперь в нём 5 литров, а сосуд 5 литров пустой.
Шаг 3. Опять наливаем в сосуд 5 л. воду. В сосуде 7 л сейчас налито 5 л воды, значит есть ещё место для двух литров.
Шаг 4. Переливаем воду из сосуда 5 л в сосуд 7 л, пока он не наполнится до краёв. Те самым мы нальём в него ровно 2 л, т.к. в нём уже было 5 л, и оставалось ещё место для 2 л воды.
Раз мы из сосуда 5 л отлили 2 л, то в нём осталось 3 л. Задача решена.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Задача
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов получить 1 л воды?
Изобразим решение на схеме. Прямоугольники означают сосуды, синий цвет - воду в сосудах. Под прямоугольниками - объём сосуда, над прямоугольником - объём воды в нём.

Пояснение к решению.
1 л воды можно получить, если из трёхлитрового сосуда отлить 2 литра воды. Значит нам надо добиться такой ситуации, когда в пятилитровом будем 3 литра воды, тем самым останется место ровно для двух литров, которые мы сможем перелить из трёхлитрового сосуда.
Шаг 1. Наливаем с трёхлитровый сосуд воду до краёв, получаем 3 литра воды
Шаг 2. Переливаем эту воду в пятилитровый сосуд. Теперь в нём 3 л воды, а в трёхлитровом пусто
Шаг 3. Опять наливаем в трёхлитровый сосуд воду, теперь по 3 л воды в каждом из сосудов.
Теперь мы добились той ситуации, которая нам была нужна - в пятилитровом сосуде есть место ровно для 2 л воды, а в трёхлитровом - 3 л воды.
Шаг 4. Переливаем воду из сосуда 3 л в сосуд 5 л, пока он не заполнится до краёв. Т.к. в нём было место для 2 л воды, то ровно эти 2 л и перельются, и в сосуде 3 л останется ровно 1 л. Залача решена.
Дата публикации
Другие методические материалы по теме
Задачи раздела:
Водоём вмещает 3600 вёдер воды. Одна труба может его наполнить за 40 минут, другая - за 24 минуты, а третья - за 30 минут. За сколько времени будет наполнен водоем, если все трубы будут работать вместе?
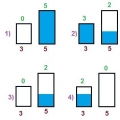
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды?

На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства. В одной из банок все монеты фальшивые. Настоящая монета весит 10 г, а фальшивая 9 г. У вас есть весы со шкалой в граммах. Как всего лишь за одно взвешивание определить, в какой из банок находятся фальшивые монеты?
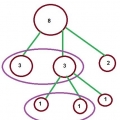
Имеется набор монет одинакового достоинства, одна из которых фальшивая.
Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243?
Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243?

Рассказываем, как в 4-5 классе решать задачи на определение фальшивой монеты за минимальное число взвешиваний.