
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Решение задач на взвешивание (определение фальшивой монеты)
Методические материалы по теме:
Рассказываем, как в 4-5 классе решать задачи на определение фальшивой монеты за минимальное число взвешиваний.
Задача
Имеется 8 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Решение этой задачи состоит в том, что исходный набор монет надо разделить на три кучки, в двух из которых число монет обязательно должно быть равным.

Если мы взвесим на весах с двумя чашами две кучки с одинаковым числом монет одинакового достоинства и одна из них окажется легче, значит фальшивая монета в этой кучке, и уже её надо разделить на три части, в двух из которых число монет обязательно должно быть равным.
Если же у взвешенных двух кучек монет одинаковый вес, значит фальшивая монета в третьей кучке.
Покажем схему взвешивания для наших 8 монет:
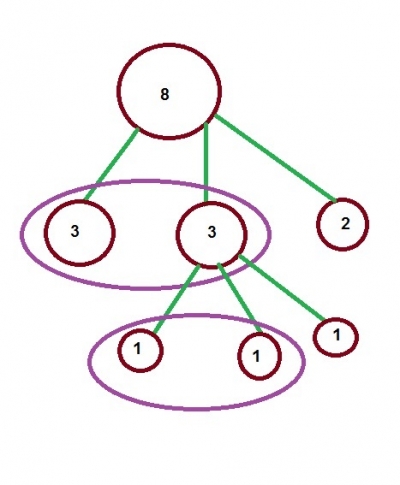
Вначале у нас есть 8 монет. Мы делим их на кучки по 3, 3 и 2 монеты.
Взвешиваем две кучки по 3 монеты. Предположим, что одна из этих кучек оказалась легче. Значит, фальшивая монета в ней. Теперь делим эту кучку на три по 1 монете в каждой.
Теперь нам достаточно взвесить любые две монеты, чтобы определить, где фальшивая - она окажется или на весах, или это будет третья монета.
Задача
Имеется 10 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. За какое минимально гарантированное количество взвешиваний можно найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Это точно такая же задача, как и предыдущая, но в ней на 2 монеты больше, и взвешиваний будет на одно больше.
Вот схема взвешивания:
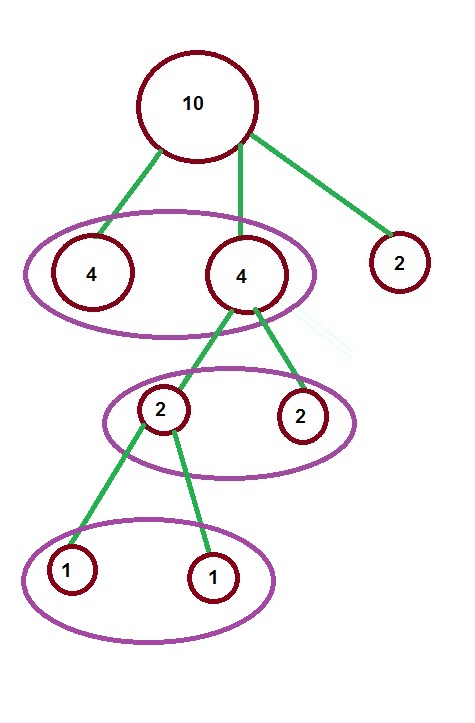
Как видим, на втором взвешивании у нас образовались кучки по две монеты, поэтому, когда мы определили, в какой из этих кучек находится фальшивая, то дальше смогли разделить её только на две "кучки" по 1 монете в каждой.
Имеется 8 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Решение этой задачи состоит в том, что исходный набор монет надо разделить на три кучки, в двух из которых число монет обязательно должно быть равным.

Если мы взвесим на весах с двумя чашами две кучки с одинаковым числом монет одинакового достоинства и одна из них окажется легче, значит фальшивая монета в этой кучке, и уже её надо разделить на три части, в двух из которых число монет обязательно должно быть равным.
Если же у взвешенных двух кучек монет одинаковый вес, значит фальшивая монета в третьей кучке.
Покажем схему взвешивания для наших 8 монет:

Вначале у нас есть 8 монет. Мы делим их на кучки по 3, 3 и 2 монеты.
Взвешиваем две кучки по 3 монеты. Предположим, что одна из этих кучек оказалась легче. Значит, фальшивая монета в ней. Теперь делим эту кучку на три по 1 монете в каждой.
Теперь нам достаточно взвесить любые две монеты, чтобы определить, где фальшивая - она окажется или на весах, или это будет третья монета.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Задача
Имеется 10 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. За какое минимально гарантированное количество взвешиваний можно найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Это точно такая же задача, как и предыдущая, но в ней на 2 монеты больше, и взвешиваний будет на одно больше.
Вот схема взвешивания:

Как видим, на втором взвешивании у нас образовались кучки по две монеты, поэтому, когда мы определили, в какой из этих кучек находится фальшивая, то дальше смогли разделить её только на две "кучки" по 1 монете в каждой.
Дата публикации
Другие методические материалы по теме
Задачи раздела:
Водоём вмещает 3600 вёдер воды. Одна труба может его наполнить за 40 минут, другая - за 24 минуты, а третья - за 30 минут. За сколько времени будет наполнен водоем, если все трубы будут работать вместе?
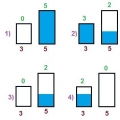
Имеется два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить 4 л воды?
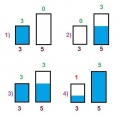
Рассказываем, как в 4-5 классе решать задачи на переливание из одного сосуда в другой.

На столе стоят десять одинаковых банок, в каждой из них по 10 монет одного достоинства. В одной из банок все монеты фальшивые. Настоящая монета весит 10 г, а фальшивая 9 г. У вас есть весы со шкалой в граммах. Как всего лишь за одно взвешивание определить, в какой из банок находятся фальшивые монеты?
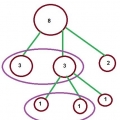
Имеется набор монет одинакового достоинства, одна из которых фальшивая.
Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243?
Сколько взвешиваний для определения фальшивой монеты надо, если монет от 28 до 81, и от 82 до 243?