
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Решение задач на чётность и нечётность
Рассказываем, как в 4 и 5 классе решать задачи, где роль играет чётность и нечётность чисел.
Для начала вспомним свойства чётных и нечётных чисел.
1. Чётные числа делятся на 2 без остатка.
0, 2, 4, 6, 8, 10... – чётные числа.
2. Нечётные числа не делятся на 2 без остатка.
1, 3, 5, 7, 9, 11... – нечётные числа
3. У чётного числа последняя цифра всегда чётная.
110, 679232, 1000008 – чётные числа
4. У нечётного числа последняя цифра всегда нечётная.
123, 974341, 5234459 – нечётные числа
5. Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный
6∙5∙11 = 330, 4∙13∙15∙21 = 16380
6. Если в произведении нескольких чисел все числа нечётные, то результат всегда нечётный
3∙17∙7 = 357, 11∙23∙65 = 16445
7. Чётные числа при сложении и вычитании всегда дают чётное число.
22 + 46 = 68, 6 + 8 + 224 + 1284 = 1522, 56-44 = 12, 120 - 32 - 48 - 6 = 34
8. Сумма чётного количества нечётных чисел всегда чётная.
13 + 15 = 28, 7 + 9 + 21 + 33 = 70, 789 + 1003 + 611 + 1893 = 4296
9. Сумма нечётного количества нечётных чисел всегда нечётная.
11 + 21 + 43 = 65, 731 + 19 + 893 + 73 + 55 = 1771
10. При вычитании из нечётного числа нечётного всегда получается чётное.
13 – 7 = 6, 93 – 39 = 54
11. При вычитании из нечётного числа чётного всегда получается нечётное.
41 – 16 = 25, 139 – 122 = 17
12. При вычитании из чётного числа нечётного всегда получается нечётное.
20 – 9 = 11, 244 – 51 = 193
Задача 1
Петя купил в магазине 10 игрушек. Игрушки стоили 321, 259 и 411 рубль. Мог ли Петя заплатить за все 10 игрушек 3311 рублей?
Решение
Для решения этой задачи нам не нужно знать, сколько именно игрушек куплено за каждую из этих цен. Достаточно вспомнить свойство 8 из вышеприведённого списка свойств чётных и нечётных чисел: "Сумма чётного количества нечётных чисел всегда чётная".
Куплено 10 игрушек, каждая из которых имеет нечётную цену. Таким образом, т.к. 10 - чётное число, а все цены нечётные, то мы имеем сумму чётного количества нечётных чисел, то есть эта сумма должна быть чётной. Но число 3311 - нечётное, поэтому 10 игрушек не могут столько стоить.
Ответ: нет, не мог, так как сумма его покупки должна быть чётным числом
Задача 2
Вася купил в магазине несколько пирожных по 50 рублей, 2 коробки конфет, несколько йогуртов по 60 рублей. Продавец сказал, что Вася должен заплатить 931 рубль. Вася возмутился и сказал, что продавец не умеет считать. Действительно ли продавец ошибся?
Решение
У нас неизвестно либо количество купленного товара (несколько пирожных и несколько йогуртов), либо цена (цена конфет). Но то, что нам известно – цена пирожных (50 руб.), цена йогуртов (60 руб.) и количество коробок конфет (2 шт.) говорит о том, что если по отдельности посчитать суммарную стоимость пирожных, йогуртов и конфет, то везде получатся чётные суммы. Вспомним свойство 5 - "Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный". Именно поэтому у нас везде будут чётные суммы.
И сложение этих чётных сумм тоже должно дать чётную сумму (свойство 7), а продавец насчитал нечётную.
Ответ: да, продавец ошибся, потому что сумма покупок должна быть чётным числом, а 931 руб. – нечётное число.
Свойства чётных и нечётных чисел
1. Чётные числа делятся на 2 без остатка.
0, 2, 4, 6, 8, 10... – чётные числа.
2. Нечётные числа не делятся на 2 без остатка.
1, 3, 5, 7, 9, 11... – нечётные числа
3. У чётного числа последняя цифра всегда чётная.
110, 679232, 1000008 – чётные числа
4. У нечётного числа последняя цифра всегда нечётная.
123, 974341, 5234459 – нечётные числа
5. Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный
6∙5∙11 = 330, 4∙13∙15∙21 = 16380
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
6. Если в произведении нескольких чисел все числа нечётные, то результат всегда нечётный
3∙17∙7 = 357, 11∙23∙65 = 16445
7. Чётные числа при сложении и вычитании всегда дают чётное число.
22 + 46 = 68, 6 + 8 + 224 + 1284 = 1522, 56-44 = 12, 120 - 32 - 48 - 6 = 34
8. Сумма чётного количества нечётных чисел всегда чётная.
13 + 15 = 28, 7 + 9 + 21 + 33 = 70, 789 + 1003 + 611 + 1893 = 4296
9. Сумма нечётного количества нечётных чисел всегда нечётная.
11 + 21 + 43 = 65, 731 + 19 + 893 + 73 + 55 = 1771
10. При вычитании из нечётного числа нечётного всегда получается чётное.
13 – 7 = 6, 93 – 39 = 54
11. При вычитании из нечётного числа чётного всегда получается нечётное.
41 – 16 = 25, 139 – 122 = 17
12. При вычитании из чётного числа нечётного всегда получается нечётное.
20 – 9 = 11, 244 – 51 = 193
Задача 1
Петя купил в магазине 10 игрушек. Игрушки стоили 321, 259 и 411 рубль. Мог ли Петя заплатить за все 10 игрушек 3311 рублей?
Решение
Для решения этой задачи нам не нужно знать, сколько именно игрушек куплено за каждую из этих цен. Достаточно вспомнить свойство 8 из вышеприведённого списка свойств чётных и нечётных чисел: "Сумма чётного количества нечётных чисел всегда чётная".
Куплено 10 игрушек, каждая из которых имеет нечётную цену. Таким образом, т.к. 10 - чётное число, а все цены нечётные, то мы имеем сумму чётного количества нечётных чисел, то есть эта сумма должна быть чётной. Но число 3311 - нечётное, поэтому 10 игрушек не могут столько стоить.
Ответ: нет, не мог, так как сумма его покупки должна быть чётным числом
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 2
Вася купил в магазине несколько пирожных по 50 рублей, 2 коробки конфет, несколько йогуртов по 60 рублей. Продавец сказал, что Вася должен заплатить 931 рубль. Вася возмутился и сказал, что продавец не умеет считать. Действительно ли продавец ошибся?
Решение
У нас неизвестно либо количество купленного товара (несколько пирожных и несколько йогуртов), либо цена (цена конфет). Но то, что нам известно – цена пирожных (50 руб.), цена йогуртов (60 руб.) и количество коробок конфет (2 шт.) говорит о том, что если по отдельности посчитать суммарную стоимость пирожных, йогуртов и конфет, то везде получатся чётные суммы. Вспомним свойство 5 - "Если в произведении нескольких чисел есть хотя бы одно чётное число, то результат всегда чётный". Именно поэтому у нас везде будут чётные суммы.
И сложение этих чётных сумм тоже должно дать чётную сумму (свойство 7), а продавец насчитал нечётную.
Ответ: да, продавец ошибся, потому что сумма покупок должна быть чётным числом, а 931 руб. – нечётное число.
Дата публикации
Задачи раздела:

Шахматный конь, сделав несколько ходов на доске, вернулся на ту же клетку, где был изначально. Он сделал чётное или нечётное число ходов? Обоснуйте ответ.

Из книги вырваны 17 листов. Может ли сумма номеров страниц на вырванных листах быть чётной?

В школе два равных по численности 11-х класса объединились, чтобы проголосовать за один из двух вариантов места проведения выпускного вечера. Голосовали все ученики. Было объявлено, что с перевесом в 5 голосов победил второй вариант. Отличник Василий, хорошо знающий математику, сразу же сказал, что голоса подсчитаны неверно. Как он это определил?
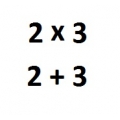
Существует ли два натуральных числа, сумма и произведение которых были бы нечётны? Обоснуйте ответ.

Можно ли разменять 35 евро 12-ю монетами по 1, 3 и 5 евро?