Тест на уровень знаний
Подберите задачи для теста по своим критериям.
Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
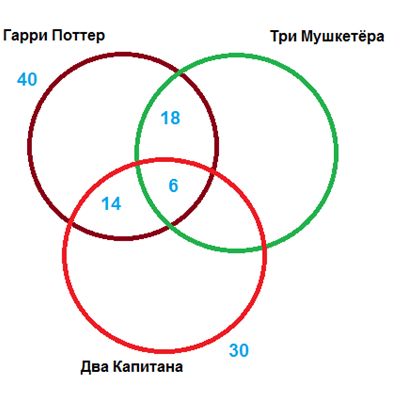
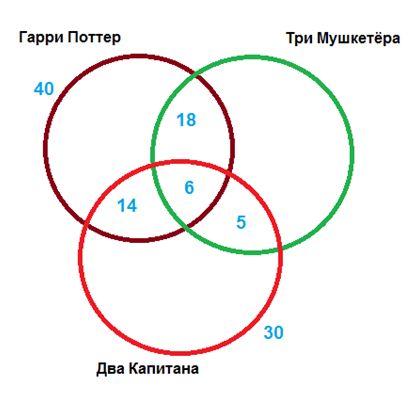
Задача: Среди 50-ти школьников провели опрос про их любимые книги
Методические материалы по теме:
Условие задачи
Среди 50-ти школьников провели опрос про их любимые книги. Список самых популярных возглавили «Гарри Поттер», «Три мушкетёра» и «Два капитана». «Гарри Поттера» назвали 40 человек, из них ещё 18 назвали «Три мушкетёра», а 14 – «Два капитана». Все три книги назвали 6 человек. «Два капитана» выбрали 30 человек, из них 19 назвали две книги из этого списка. Сколько человек выбрали «Три мушкетёра»?
Раскрыть решение
Методические материалы по теме
Задачи раздела:
В семье жучков 18 мальчиков, а остальные девочки. 10 жучков носят панамки, а остальные кепки. Оказалось, что девочек носящих кепки, столько же, сколько мальчиков носящих панамки. Сколько всего детей в семье жучков?
Капа готовит пирожки для 28 местных жителей. Известно, что каждый житель хоть какой-то вид пирожков да любит, а может и все сразу. Она знает, что 18 жителей предпочитают пироги с морошкой, 14 с клубникой, а 12 с черникой. При этом пироги с морошкой и с клубникой предпочитают 9 жителей. Пироги с морошкой и черникой 7 жителей, а с клубникой и черникой 5. Сколько местных жителей, которые любят все 3 вида пирожков?
Кузнечик Кузя захотел узнать, кого больше: кузнечиков, кроме тех, которых не зовут Кузями, или Кузь, кроме тех Кузей, кто не является кузнечиками. Помогите Кузе разобраться в этом вопросе.
Лунтик, Кузя, Мила и Пчеленок сделали бумажные кораблики. Они посчитали, что если сложить кораблики Кузи, Милы и Пчеленка, то у них получится 7 корабликов, если сложить кораблики, которые сделали Лунтик, Мила и Пчеленок то получится 6 корабликов, а если сложить кораблики без Милиных, то 8, а если без корабликов Пчеленка, то 9. Сколько всего бумажных корабликов сделал один Лунтик?
250 муравьев тащили в муравейник ягоды. Известно, что каждый муравей, который принес малину, принес и землянику. Малину не принесли 200 муравьев, а землянику не принесли 170 муравьев. Кого больше и на сколько: муравьев, которые принесли малину, или муравьев, которые принесли землянику, но не принесли малину?
Мила сказала Пчеленку, что у нее много подружек, среди их точно есть хоть одна бабочка, гусеница и стрекоза. Она сказала, что все, кто придут к ней в гости сегодня, кроме двоих, будут бабочками. Также все, кто придет к ней сегодня в гости, кроме двоих, будут гусеницами. Остальные же, кто придет в гости к ней будут стрекозами. Сколько подружек придет к Миле в гости?
Лунтик попросил Пчеленка научить его считать до 210. А в качестве поощрения за труд, Пчеленок говорил Лунтику «молодец», каждый раз, когда Лунтик называл числа, которые не делятся ни на 3, ни на 7. Сколько раз Лунтика назвали «молодец»?
Из улья отправилось 45 пчел собирать нектар на цветочную поляну, а 58 пчел собирать нектар везде, но только с клевера. При этом из улья всего вылетело 71 пчела. Пчеленок был среди них, но он отпросился к Лунтику по делам. Сколько пчел отправилось собирать нектар на цветочную поляну с клевера?
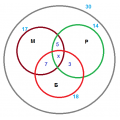
В классе 30 человек. Из них 17 ходят в кружок по математике, 14 – в кружок по робототехнике и 18 – в кружок по биологии. Одновременно на математику и робототехнику ходят 5, на математику и биологию - 7, на робототехнику и биологию - 3. Четверо не ходят ни на какие из этих кружков. Сколько учеников ходит на 3 кружка одновременно? Сколько учеников ходит только в один кружок?
Показываем, как решать задачи на множества в 4-5 классе.
