
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Задачи на множества
Множество - это группа предметов (людей, понятий) с общими свойствами и собранных вместе. Предметы любого множества называют элементами множества.
Лучше всего знакомство со множествами начать с решения простых задач.
Задача 1. На выходных ученики ходили в кино. 20 из них посмотрели фильм «Завод», 13 смотрели фильм «Хеллбой» из них 8 посмотрели оба фильма. Сколько учеников посмотрело только фильм «Завод»?
Для решения этой задачи нам помогут круги Эйлера. С помощью этих кругов можно показать отношения между каким-либо множеством и его частью. Леонард Эйлер, в честь которого названы эти круги - это швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Он родился в Швейцарии, но почти половину жизни провёл в России, поэтому он считается не только швейцарским математиком, но и российским.
Нарисуем схему:
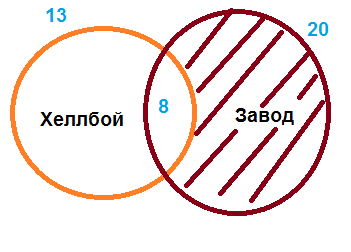
Круг "Хеллбой" - те, кто посмотрели этот фильм. Над ним число 13 - количество посмотревших.
Круг "Завод" - те, кто посмотрел фильм "Завод". Над ним число 20 - количество посмотревших.
Эти круги пересекаются и в месте пересечения число 8 - количество тех, кто посмотрел оба этих фильма. Это число 8 входит и в число 13 - посмотревших "Хеллбой", и в число 20 - посмотревших "Завод".
Из схемы хорошо видно, что посмотревшие только фильм "Завод", и не посмотревшие фильм "Хеллбой" - находятся в заштрихованной зоне круга "Завод". В эту зону не входят те 8 человек, которые посмотрели и "Хеллбой" и "Завод".
Таким образом, эта задача решается в одно действие: из 20 человек, посмотревших "Завод", надо вычесть 8 человек, которые посмотрели и "Завод" и "Хеллбой", и тем самым мы получим число тех, кто посмотрел только "Завод".
20 - 8 = 12 человек
Ответ: 12 человек
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Задача 2. В овощной магазин за 1 час зашло 20 человек. Из них 12 купили картошку, 5 – лук, 7 не купили ничего. Сколько человек купили и картошку и лук?
Как вы уже наверное поняли из предыдущей задачи, такого рода задачи можно решить и без рисования кругов Эйлера.
Решение
1. Найдём общее число покупателей. Для этого из тех 20 человек, которые зашли в магазин, вычтем те 7 человек, которые ничего не купили.
20 – 7 = 13
2. Найдём число тех, кто купил только лук
Для этого из 13-ти купивших вычтем 12 человек, которые купили картошку. Останутся те люди, которые купили только лук и не купили картошку.
13 – 12 = 1
3. Найдём число тех, кто купил и картошку и лук
В множество тех людей, кто купил лук, входят те, кто купил и картошку и лук и те, кто купил только лук.
Число тех, кто купил только лук, мы нашли во втором действии - это 1 чеовек.
5 – 1 = 4 - число тех, кто купил и картошку и лук.
Ответ: 4
Задача 3. В классе 27 учеников. Из них 16 занимаются плаванием, 10 – футболом, а 5 не занимаются ни тем, ни другим. Сколько футболистов ходит ещё и на плавание?
Решение
Для решения этой задачи нарисуем круги Эйлера, хотя задачу можно решить и без них.
Буквой "П" обозначим множество тех, кто занимается плаванием, буквой "Ф" - тех, кто занимается футболом. П+Ф - те, кто занимаются и плаванием и футболом.
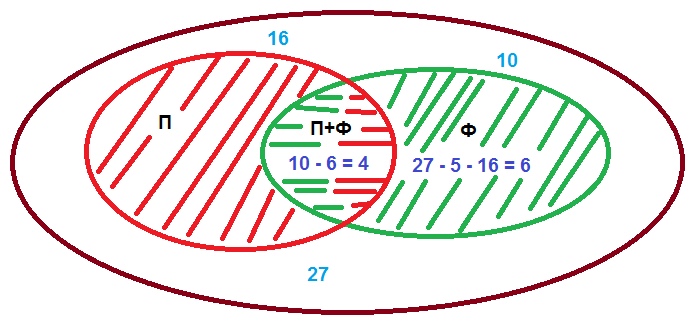
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Если мы вычтем из общего числа учеников (27) число тех, кто не занимается ни плаванием, ни футболом, то мы получим число тех, кто занимаются плаванием, футболом или и тем и другим.
1. Найдём число учеников, которые занимаются плаванием, футболом или и тем и другим
27 – 5 = 22
2. Найдём количество футболистов, которые не ходят на плавание
22 – 16 = 6
3. Найдём количество футболистов, которые ходят ещё и на плавание
В предыдущем действии мы наши число учеников, которые занимаются только футболом.
Таким образом, чтобы найти число учеников, которые занимаются и футболом, и плаванием, надо из общего числа футболистов вычесть тех, кто занимается только футболом (6).
10 – 6 = 4
Ответ: 4
Дата публикации
Задачи раздела:
Среди 50-ти школьников провели опрос про их любимые книги. Список самых популярных возглавили «Гарри Поттер», «Три мушкетёра» и «Два капитана». «Гарри Поттера» назвали 40 человек, из них ещё 18 назвали «Три мушкетёра», а 14 – «Два капитана». Все три книги назвали 6 человек. «Два капитана» выбрали 30 человек, из них 19 назвали две книги из этого списка. Сколько человек выбрали «Три мушкетёра»?
В классе 30 человек. Из них 17 ходят в кружок по математике, 14 – в кружок по робототехнике и 18 – в кружок по биологии. Одновременно на математику и робототехнику ходят 5, на математику и биологию - 7, на робототехнику и биологию - 3. Четверо не ходят ни на какие из этих кружков. Сколько учеников ходит на 3 кружка одновременно? Сколько учеников ходит только в один кружок?