Нахождение внутренних перегородок в прямоугольнике, разделённом на клетки

Задача 1

Суммарная длина перегородок в клетчатом прямоугольнике 4 × 5 на рисунке равна 31. Чему равна суммарная длина перегородок в прямоугольнике 12 × 50? (Задача из вступительных экзаменов в 5 класс ФМЛ 239 за 2017 г )

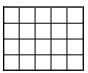
Решение

Несложно увидеть, что количество внутренних линий, идущих от края до края – как вертикальных, так и горизонтальных, на 1 меньше, чем число клеток по горизонтали и вертикали соответственно.

По вертикали в этом прямоугольнике 4 клетки и 3 внутренних горизонтальных линии, а по горизонтали 5 клеток и 4 внутренних вертикальных линии.
На каждой вертикальной линии 4 перегородки (т.к. 4 клетки по вертикали), на каждой горизонтальной линии 5 перегородок (т.к. 5 клеток по горизонтали)

число вертикальных перегородок: 4∙4 = 16
число горизонтальных перегородок: 3∙5 = 15

Таким образом, общее число горизонтальных и вертикальных перегородок = 16 + 15 = 31 – что как раз соответствует суммарной длине перегородок из условия задачи. Очевидно, в данном случае это обусловлено тем, что все клетки являются одинаковыми квадратами.

Для прямоугольника 12x50, равно как и для любого другого будет выполняться то же правило - количество внутренних линий, идущих от края до края – как вертикальных, так и горизонтальных, на 1 меньше, чем число клеток по горизонтали и вертикали соответственно.
Таким образом, в прямоугольнике 12x50 имеется 11 горизонтальных линий и 49 вертикальных.

число вертикальных перегородок: 49∙12 = 588
число горизонтальных перегородок: 11∙50 = 550

Общее число горизонтальных и вертикальных перегородок = 588+550 = 1138

Ответ: 1138

Задача 2

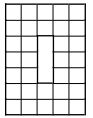
На рисунке изображена буква О ширины 5, высоты 7, толщины 2 клетки. Суммарная длина её внутренних перегородок равна 48. Чему равна суммарная длина внутренних перегородок буквы О, у которой толщина 4, высота 40, ширина 30 клеток? (Задача из вступительных экзаменов в 5 класс ФМЛ 239, 2018 г)

Решение

Эту задачу можно решить двумя способами:

1. Найти, как число внутренних перегородок зависит от размера «дырки» внутри буквы О, т.е. от толщины

2. Воспользовавшись методикой из предыдущей задачи, найти, сколько перегородок должно быть внутри буквы «О», если бы в ней не было дырки, и вычесть число внутренних перегородок внутри дырки, если бы они там были, а также вычесть внешние края буквы О, которые тоже не являются внутренними перегородками

Мы применим второй способ. Для начала проверим его на исходной букве «О» размером 5x7 и толщиной 2 клетки.

Число вертикальных линий – 4 (на 1 меньше, чем число клеток по горизонтали )
Число горизонтальных линий – 6 (на 1 меньше, чем число клеток по вертикали)


Если бы внутри буквы «О» не было бы дырки, то мы имели бы прямоугольник со следующим числом внутренних перегородок:

число вертикальных перегородок: 4∙7 = 28
число горизонтальных перегородок: 6∙5 = 30

Общее число внутренних перегородок: 28 + 30 = 58

Теперь рассмотрим дырку от буквы «О». Её размеры 3x1.
Посчитаем, сколько внутренних перегородок в ней было бы, если бы они были нарисованы

число вертикальных перегородок: 0
число горизонтальных перегородок: 2
Общее число внутренних перегородок: 2

Также нам надо учесть перегородки, составляющие внешние края дырки:
Всего таких перегородок: 2∙3 + 2∙1 = 8

Таким образом, общее число внутренних перегородок нашего исходного прямоугольника, которые пришлись на дырку, составляет 2 + 8 = 10

Таким образом, общее число внутренних перегородок внутри буквы О –
58 – 10 = 48

48 – это как раз то число, которое у нас в условии задачи, то есть мы посчитали верно.

Теперь перейдём к букве «О», у которой толщина 4, высота 40, ширина 30 клеток.


Найдём число внутренних перегородок у соответствующего прямоугольника 40x30, когда в нём нет дырки:

Число вертикальных линий – 29 (на 1 меньше, чем число клеток по горизонтали )
Число горизонтальных линий – 39 (на 1 меньше, чем число клеток по вертикали)

число вертикальных перегородок: 29∙40 = 1160
число горизонтальных перегородок: 39∙30 = 1170

Общее число внутренних перегородок – 2330

Найдём размеры дырки от буквы «О»

Чтобы найти ширину дырки, надо из общей ширины прямоугольника вычесть толщину левого и правого края, которая составляет, исходя из условия задачи, 4. Высота дырки находится аналогично, толщина верхнего и нижнего края в данном случае тоже равна 4.

Ширина дырки: 30 - 4 – 4 = 22
Высота дырки: 40 – 4 – 4 = 32

Найдём число внутренних перегородок у дырки, если бы они были нарисованы

число вертикальных перегородок: (22 – 1)∙32 = 672
число горизонтальных перегородок: (32 - 1)∙22 = 682
Общее число внутренних перегородок = 672 + 682 = 1354

Перегородки, составляющие внешние края дырки: 2∙22 + 2∙32 = 108

Общее число внутренних перегородок в букве «О»: 2330 – 1354 – 108 = 868

Ответ: 868