Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
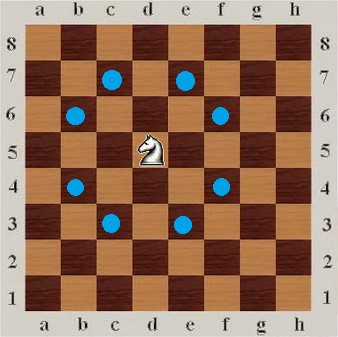
Задача: Шахматный конь, сделав несколько ходов на доске, вернулся на ту же клетку, где был изначально
Методические материалы по теме:
Условие задачи
Шахматный конь, сделав несколько ходов на доске, вернулся на ту же клетку, где был изначально. Он сделал чётное или нечётное число ходов? Обоснуйте ответ.
Раскрыть решение
Методические материалы по теме
Задачи раздела:

Из книги вырваны 17 листов. Может ли сумма номеров страниц на вырванных листах быть чётной?

В школе два равных по численности 11-х класса объединились, чтобы проголосовать за один из двух вариантов места проведения выпускного вечера. Голосовали все ученики. Было объявлено, что с перевесом в 5 голосов победил второй вариант. Отличник Василий, хорошо знающий математику, сразу же сказал, что голоса подсчитаны неверно. Как он это определил?
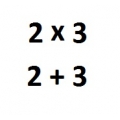
Существует ли два натуральных числа, сумма и произведение которых были бы нечётны? Обоснуйте ответ.

Можно ли разменять 35 евро 12-ю монетами по 1, 3 и 5 евро?
Рассказываем, как в 4 и 5 классе решать задачи, где роль играет чётность и нечётность чисел.