
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Задача: Сколько существует трехзначных чисел, у которых все цифры четные?
Методические материалы по теме:
Условие задачи
Сколько существует трехзначных чисел, у которых все цифры четные? Сколько существует трехзначных чисел, у которых все цифры четные и при этом разные?
Раскрыть решение
Методические материалы по теме
Задачи раздела:
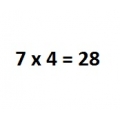
Сколько существует чётных пятизначных чисел с произведением цифр, равным 28?

12 бегунов требуется разбить на 3 равные группы по 4 бегуна в каждой. Сколькими способами это можно сделать?

Сколько существует пятизначных чисел, у которых вторая цифра 2, а третья цифра нечетная?

1. В соревнованиях по плаванию участвуют четыре человека.
Сколько существует вариантов распределения мест между ними?
2. Сколькими способами можно рассадить 4 человек за столом?
Сколько существует вариантов распределения мест между ними?
2. Сколькими способами можно рассадить 4 человек за столом?

В туристической группе 10 человек. Необходимо выбрать начальника группы и его заместителя. Сколько существует вариантов это сделать?
Комбинаторика - раздел математики, который изучает комбинации и перестановки предметов, расположение элементов в соответствии с заданными правилами.