
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Комбинаторика. Вводный урок
Комбинаторика - раздел математики, который изучает комбинации и перестановки предметов, расположение элементов в соответствии с заданными правилами.
В этом уроке мы расскажем, как решать задачи на комбинаторику в 4 и 5 классах.
Пусть у нас есть по разному составленные наборы из красного, чёрного и зелёного кубиков. В первом случае два кубика, во втором и третьем - по три кубика. Укажем, сколькими способами можно выбрать один из кубиков:

Это правило называется правилом сложения. Число способов выбрать один элемент из набора разнотипных элементов (в нашем случае – кубики разного цвета) равно сумме числа элементов в каждом из наборов. Например, если зелёных кубиков один, а чёрных кубиков два, то способов выбрать или один зелёный кубик, или один чёрный равно 3 (1 + 2).
Сколько есть способов поставить разноцветные кубики один на другой?
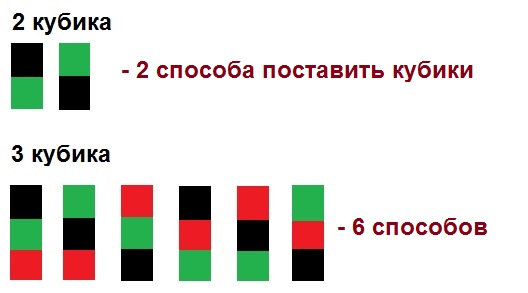
Как можно математически подсчитать число комбинаций для 3-х кубиков?
Когда мы ставим первый кубик, у нас есть 3 варианта – кубики всех трёх цветов.
Когда мы ставим второй кубик, у нас есть 2 варианта, т.к. один цвет уже задействовали в первом кубике.
Когда мы ставим третий кубик, у нас есть 1 вариант, т.к. остался только один кубик.
Число способов поставить один кубик на другой = 3∙2∙1 = 6
Это правило называется правилом умножения. Для подсчёта числа комбинаций из нескольких элементов надо перемножить число вариантов для каждого элемента.
Ответ на этот простой вопрос вы и так знаете – двузначных чисел всего 90.
Эти же 90 можно получить по правилам комбинаторики.
Для первой цифры двузначного числа есть 9 вариантов (1..9, 0 первой цифрой быть не может)
Для второй цифры двузначного числа есть 10 вариантов (0..9 – тут уже могут быть все 10 цифр, включая 0)
Общее число двузначных чисел: 9∙10 = 90 - тут мы использовали правило умножения.
Как видите, метод подсчёта числа комбинаций разноцветных кубиков такой же, как для подсчёта количества двузначных чисел.
Для первой цифры есть 8 вариантов (0 не может быть первой цифрой, 5 не может быть по условию).
Для второй цифры есть 9 вариантов (5 не может быть по условию).
Для третьей цифры есть 9 вариантов (5 не может быть по условию).
Общее число трёхзначных чисел без 5: 8∙9∙9 = 648
Если бы нам надо было посчитать все трёхзначные числа, где есть хотя бы одна 5, то мы сначала посчитали бы все трёхзначные числа, где нет ни одной 5 (648), а потом из общего числа трёхзначных чисел (900) вычли бы 648. Получили бы 900 – 648 = 252.
Из Саратова в Волгоград можно добраться на поезде, на самолёте, на автомобиле и на теплоходе по Волге. Сколько всего есть способов добраться из Саратова в Волгоград и вернуться обратно, если учесть, что все способы работают в обеих направлениях.
Решение
Существует 4 способа добраться из Саратова в Волгоград и 4 способа вернуться обратно из Волгограда в Саратов. Соответственно, применяя правило умножения, мы можем сказать, что существует 4∙4 = 16 способов добраться из Саратова в Волгоград и вернуться обратно.
Проверим наше решение, перечислив все возможные способы:
1. на самолёте в Волгоград и на самолёте обратно в Саратов
2. на самолёте в Волгоград и на поезде обратно в Саратов
3. на самолёте в Волгоград и на автомобиле обратно в Саратов
4. на самолёте в Волгоград и на теплоходе обратно в Саратов
5. на поезде в Волгоград и на самолёте обратно в Саратов
6. на поезде в Волгоград и на поезде обратно в Саратов
7. на поезде в Волгоград и на автомобиле обратно в Саратов
8. на поезде в Волгоград и на теплоходе обратно в Саратов
9. на автомобиле в Волгоград и на самолёте обратно в Саратов
10. на автомобиле в Волгоград и на поезде обратно в Саратов
11. на автомобиле в Волгоград и на автомобиле обратно в Саратов
12. на автомобиле в Волгоград и на теплоходе обратно в Саратов
13. на теплоходе в Волгоград и на самолёте обратно в Саратов
14. на теплоходе в Волгоград и на поезде обратно в Саратов
15. на теплоходе в Волгоград и на автомобиле обратно в Саратов
16. на теплоходе в Волгоград и на теплоходе обратно в Саратов
Как видим, всего 16 вариантов - ровно столько, сколько мы получили в одно действие по правилу умножения.
Знанием комбинаторики значительно ускоряет расчёты в задачах на комбинации.
Вычисление числа способов выбрать один из кубиков
Пусть у нас есть по разному составленные наборы из красного, чёрного и зелёного кубиков. В первом случае два кубика, во втором и третьем - по три кубика. Укажем, сколькими способами можно выбрать один из кубиков:

Это правило называется правилом сложения. Число способов выбрать один элемент из набора разнотипных элементов (в нашем случае – кубики разного цвета) равно сумме числа элементов в каждом из наборов. Например, если зелёных кубиков один, а чёрных кубиков два, то способов выбрать или один зелёный кубик, или один чёрный равно 3 (1 + 2).
Вычисление числа способов комбинировать несколько кубиков
Сколько есть способов поставить разноцветные кубики один на другой?

Как можно математически подсчитать число комбинаций для 3-х кубиков?
Когда мы ставим первый кубик, у нас есть 3 варианта – кубики всех трёх цветов.
Когда мы ставим второй кубик, у нас есть 2 варианта, т.к. один цвет уже задействовали в первом кубике.
Когда мы ставим третий кубик, у нас есть 1 вариант, т.к. остался только один кубик.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Число способов поставить один кубик на другой = 3∙2∙1 = 6
Это правило называется правилом умножения. Для подсчёта числа комбинаций из нескольких элементов надо перемножить число вариантов для каждого элемента.
Сколько существует двузначных чисел?
Ответ на этот простой вопрос вы и так знаете – двузначных чисел всего 90.
Эти же 90 можно получить по правилам комбинаторики.
Для первой цифры двузначного числа есть 9 вариантов (1..9, 0 первой цифрой быть не может)
Для второй цифры двузначного числа есть 10 вариантов (0..9 – тут уже могут быть все 10 цифр, включая 0)
Общее число двузначных чисел: 9∙10 = 90 - тут мы использовали правило умножения.
Как видите, метод подсчёта числа комбинаций разноцветных кубиков такой же, как для подсчёта количества двузначных чисел.
Сколько существует трёхзначных чисел, в которых нет ни одной 5?
Для первой цифры есть 8 вариантов (0 не может быть первой цифрой, 5 не может быть по условию).
Для второй цифры есть 9 вариантов (5 не может быть по условию).
Для третьей цифры есть 9 вариантов (5 не может быть по условию).
Общее число трёхзначных чисел без 5: 8∙9∙9 = 648
Если бы нам надо было посчитать все трёхзначные числа, где есть хотя бы одна 5, то мы сначала посчитали бы все трёхзначные числа, где нет ни одной 5 (648), а потом из общего числа трёхзначных чисел (900) вычли бы 648. Получили бы 900 – 648 = 252.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача
Из Саратова в Волгоград можно добраться на поезде, на самолёте, на автомобиле и на теплоходе по Волге. Сколько всего есть способов добраться из Саратова в Волгоград и вернуться обратно, если учесть, что все способы работают в обеих направлениях.
Решение
Существует 4 способа добраться из Саратова в Волгоград и 4 способа вернуться обратно из Волгограда в Саратов. Соответственно, применяя правило умножения, мы можем сказать, что существует 4∙4 = 16 способов добраться из Саратова в Волгоград и вернуться обратно.
Проверим наше решение, перечислив все возможные способы:
1. на самолёте в Волгоград и на самолёте обратно в Саратов
2. на самолёте в Волгоград и на поезде обратно в Саратов
3. на самолёте в Волгоград и на автомобиле обратно в Саратов
4. на самолёте в Волгоград и на теплоходе обратно в Саратов
5. на поезде в Волгоград и на самолёте обратно в Саратов
6. на поезде в Волгоград и на поезде обратно в Саратов
7. на поезде в Волгоград и на автомобиле обратно в Саратов
8. на поезде в Волгоград и на теплоходе обратно в Саратов
9. на автомобиле в Волгоград и на самолёте обратно в Саратов
10. на автомобиле в Волгоград и на поезде обратно в Саратов
11. на автомобиле в Волгоград и на автомобиле обратно в Саратов
12. на автомобиле в Волгоград и на теплоходе обратно в Саратов
13. на теплоходе в Волгоград и на самолёте обратно в Саратов
14. на теплоходе в Волгоград и на поезде обратно в Саратов
15. на теплоходе в Волгоград и на автомобиле обратно в Саратов
16. на теплоходе в Волгоград и на теплоходе обратно в Саратов
Как видим, всего 16 вариантов - ровно столько, сколько мы получили в одно действие по правилу умножения.
Знанием комбинаторики значительно ускоряет расчёты в задачах на комбинации.
Дата публикации
Задачи раздела:
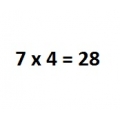
Сколько существует чётных пятизначных чисел с произведением цифр, равным 28?

12 бегунов требуется разбить на 3 равные группы по 4 бегуна в каждой. Сколькими способами это можно сделать?

Сколько существует пятизначных чисел, у которых вторая цифра 2, а третья цифра нечетная?

Сколько существует трехзначных чисел, у которых все цифры четные? Сколько существует трехзначных чисел, у которых все цифры четные и при этом разные?

1. В соревнованиях по плаванию участвуют четыре человека.
Сколько существует вариантов распределения мест между ними?
2. Сколькими способами можно рассадить 4 человек за столом?
Сколько существует вариантов распределения мест между ними?
2. Сколькими способами можно рассадить 4 человек за столом?

В туристической группе 10 человек. Необходимо выбрать начальника группы и его заместителя. Сколько существует вариантов это сделать?