
Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Решение задач, связанных с датами и календарём
Показываем, как в 4-5 классе решать задачи, связанные с календарем, датами и днями недели.
Если ваш ребёнок отправляется на экзамен или олимпиаду, где могут быть задачи, связанные с календарём, убедитесь, что он знает, сколько дней в каждом месяце, помнит про високосные года - что високосный год это тот, который без остатка делится на 4, и что у високосного года в феврале 29 дней, а дней в году 366. Это критически важно для таких задач. На экзамене подсмотреть в календарь в смартфоне будет нельзя.
А теперь на конкретных примерах рассмотрим, как решать такие задачи.
Решение
В каждом месяце 4 полных недели (28 дней) и, если это не февраль, то ещё 2 или 3 дня. Если это февраль високосного года, то ещё 1 день. Таким образом, в каждом месяце гарантированно 4 раза встречается каждый день недели, и ещё 2 или 3 дня недели могут встречаться 5 раз.
Очевидно, что для того, чтобы какой-то день недели гарантированно (кроме февраля) был в месяце 5 раз, надо чтобы первое число этого месяца приходилось на этот день недели, в крайнем случае второе число.
Нам надо ответить на вопрос, могут ли в одном месяце одновременно быть 5 четвергов, 5 суббот и 5 воскресений.
Вариант 1. Месяц начинается с понедельника:
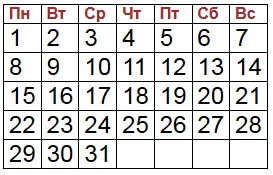
Вариант 2. Месяц начинается с четверга:
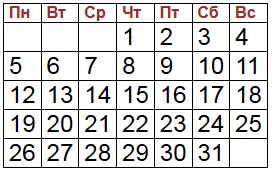
Если первое число месяца приходится на четверг, то пятый четверг приходится на 1 + 7∙4 = 1 + 28 = 29 число.
После этого ещё будет одна пятница 30-го числа, и, если в месяце 31 день, то одна суббота.
Т.к. нет месяцев, в которых 32 дня, то 5 четвергов и 5 воскресений быть не может.
Ответ: 5 четвергов и 5 суббот может быть только если в месяце 31 день, и первое число приходится на четверг. 5 четвергов и 5 воскресений быть не может.
Решение
2008 – это високосный год, т.е в феврале 29 дней. 5 пятниц может быть только при условии, что 1 февраля приходится на пятницу (вспомним решение предыдущей задачи). Тогда последняя пятница – это 1 + 7∙4 = 29 февраля. Таким образом, если 29 февраля – пятница, то 22 февраля тоже пятница (29 – 7 = 22). Таким образом, 21 февраля – четверг.
Ответ: четверг
Проверка:
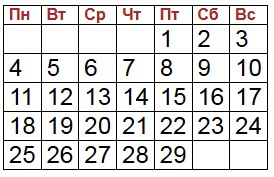
Решение
Во-первых, вспомним, что в каждом месяце может быть максимум 5 одинаковых дней недели. И вспомним, что чётное число при сложении с нечётным даёт нечётное число. Так как в неделе 7 дней, то чётные субботы (приходящиеся на чётные числа) чередуются с нечётными – равно как и чётные понедельники чередуются с нечётными и т.д.
То есть если у нас максимум 5 одинаковых дней недели в месяце, и из них три пришлись на чётные числа, то это значит, что самый первый такой день недели должен приходиться на чётное число. Таким образом, если у нас первая суббота – чётная, то вторая – нечётная, третья опять чётная, четвёртая нечётная и последняя пятая – чётная.
Наименьшее чётное число – это 2. То есть первый день месяца – это пятница, второй день – суббота. Таким образом, 9 число тоже суббота (2 + 7 = 9). Следовательно, 10 – это воскресение, а 11 – понедельник.
Ответ: понедельник.4
Итак, на основе решения этих задач мы можем запомнить важные правила, которые пригодятся для решения других задач, связанных с календарём:
1. В месяце гарантированно есть 4 одинаковых дня недели, и может быть максимум 5 одинаковых дней недели.
2. Для того, чтобы в месяце было 5 одинаковых дней недели, надо, чтобы этот день недели приходился на 1 или 2 число месяца. В случае, если в месяце 31 день, то он может приходиться и на 3 число (3 + 7∙4 = 31)
3. Так как в неделе 7 дней (нечётное число), то одинаковые дни недели поочерёдно выпадают на чётные и нечётные числа месяца. Не может быть такого, что два одинаковых дня недели в соседних неделях приходятся оба на чётные или оба на нечётные числа.
4. Зная, сколько всего заданных дней недели в месяце, и сколько из них пришлось на чётные или нечётные числа, мы можем понять, на какое число - чётное или нечётное выпал первый соответствующий день недели в этом месяце.
А теперь на конкретных примерах рассмотрим, как решать такие задачи.
1. Задача. Может ли в одном месяце быть 5 четвергов, 5 суббот и 5 воскресений и при каких условиях?
Решение
В каждом месяце 4 полных недели (28 дней) и, если это не февраль, то ещё 2 или 3 дня. Если это февраль високосного года, то ещё 1 день. Таким образом, в каждом месяце гарантированно 4 раза встречается каждый день недели, и ещё 2 или 3 дня недели могут встречаться 5 раз.
Очевидно, что для того, чтобы какой-то день недели гарантированно (кроме февраля) был в месяце 5 раз, надо чтобы первое число этого месяца приходилось на этот день недели, в крайнем случае второе число.
Нам надо ответить на вопрос, могут ли в одном месяце одновременно быть 5 четвергов, 5 суббот и 5 воскресений.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вам поможет наш ВИДЕОКУРС
Вариант 1. Месяц начинается с понедельника:

Вариант 2. Месяц начинается с четверга:

Если первое число месяца приходится на четверг, то пятый четверг приходится на 1 + 7∙4 = 1 + 28 = 29 число.
После этого ещё будет одна пятница 30-го числа, и, если в месяце 31 день, то одна суббота.
Т.к. нет месяцев, в которых 32 дня, то 5 четвергов и 5 воскресений быть не может.
Ответ: 5 четвергов и 5 суббот может быть только если в месяце 31 день, и первое число приходится на четверг. 5 четвергов и 5 воскресений быть не может.
2. Задача В феврале 2008 года 5 пятниц. На какой день недели приходится 21 февраля 2008 года?
Решение
2008 – это високосный год, т.е в феврале 29 дней. 5 пятниц может быть только при условии, что 1 февраля приходится на пятницу (вспомним решение предыдущей задачи). Тогда последняя пятница – это 1 + 7∙4 = 29 февраля. Таким образом, если 29 февраля – пятница, то 22 февраля тоже пятница (29 – 7 = 22). Таким образом, 21 февраля – четверг.
Ответ: четверг
Проверка:

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
3. Задача. В некотором месяце три субботы пришлись на чётные числа. Какой день недели был 11 числа этого месяца?
Решение
Во-первых, вспомним, что в каждом месяце может быть максимум 5 одинаковых дней недели. И вспомним, что чётное число при сложении с нечётным даёт нечётное число. Так как в неделе 7 дней, то чётные субботы (приходящиеся на чётные числа) чередуются с нечётными – равно как и чётные понедельники чередуются с нечётными и т.д.
То есть если у нас максимум 5 одинаковых дней недели в месяце, и из них три пришлись на чётные числа, то это значит, что самый первый такой день недели должен приходиться на чётное число. Таким образом, если у нас первая суббота – чётная, то вторая – нечётная, третья опять чётная, четвёртая нечётная и последняя пятая – чётная.
Наименьшее чётное число – это 2. То есть первый день месяца – это пятница, второй день – суббота. Таким образом, 9 число тоже суббота (2 + 7 = 9). Следовательно, 10 – это воскресение, а 11 – понедельник.
Ответ: понедельник.4
Итак, на основе решения этих задач мы можем запомнить важные правила, которые пригодятся для решения других задач, связанных с календарём:
1. В месяце гарантированно есть 4 одинаковых дня недели, и может быть максимум 5 одинаковых дней недели.
2. Для того, чтобы в месяце было 5 одинаковых дней недели, надо, чтобы этот день недели приходился на 1 или 2 число месяца. В случае, если в месяце 31 день, то он может приходиться и на 3 число (3 + 7∙4 = 31)
3. Так как в неделе 7 дней (нечётное число), то одинаковые дни недели поочерёдно выпадают на чётные и нечётные числа месяца. Не может быть такого, что два одинаковых дня недели в соседних неделях приходятся оба на чётные или оба на нечётные числа.
4. Зная, сколько всего заданных дней недели в месяце, и сколько из них пришлось на чётные или нечётные числа, мы можем понять, на какое число - чётное или нечётное выпал первый соответствующий день недели в этом месяце.
Дата публикации
Задачи раздела:
В апреле три среды пришлись на нечетные числа. Какой день недели был 25-го числа следующего месяца?
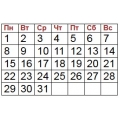
В каком-то году некоторое число ни в одном месяце не было воскресеньем. Какое это могло быть число?
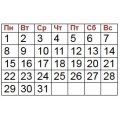
Какое самое большое число месяцев с пятью вторниками может быть в году?
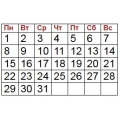
Какое наибольшее число четвергов может быть в году?