Вступительная работа по математике в 5 класс ФМЛ № 239 (Петербург). 2019 год. II вариант

1. Возраст нескольких друзей составляет в сумме 62 года. Через 4 года
он будет составлять 90 лет. Сколько этих друзей?

Ответ:

2. Сколько чисел от 239 до 457 содержат в записи одновременно цифры
3 и 4?

Ответ:

3. У какого числа от 3497029 до 3813472 самая большая сумма цифр?

Ответ:

4. Для забора нужны доски длиной 80 сантиметров в количестве 120
штук. В магазине продаются доски длиной 6 метров. Сколько досок
надо купить, чтобы построить забор?

Ответ:

5. Вычислите 189 × 3 × 307 − 63 × 3 × 920 + 737 × 293 − 736 × 292

Ответ:

6. Света, Маша и Оля разделили между собой 60 конфет. Света заметила, что если она отдаст все свои конфеты Маше, то у Маши и Оли станет поровну конфет, а если она отдаст все свои конфеты Оле, то у Оли станет в пять раз больше конфет, чем у Маши. Сколько конфет было у Светы?

Ответ:

7. В 2054 году в мае будет больше воскресений, чем понедельников. На
какой день выпадет 12 августа в том году?

Ответ:

8. На часах одной башни 6 марта, 14 часов, и время идёт правильно, а
на часах другой башни 10 марта, 8 часов, но время идёт назад. Через
сколько часов на двух башнях будут одинаковые даты и одинаковое
время?

Ответ:

9. Имеется 36 брёвен – длинных и коротких. Длинные распиливают на
6 частей, а короткие – на 5 частей. Чтобы распилить все короткие
брёвна, потребовалось сделать столько же распилов, сколько чтобы
распилить все длинные. Сколько было сделано распилов?

Ответ:

10. Антон, Борис, Василий, Георгий, Дмитрий и Евгений соревновались в решении задач. Антон пропустил вперед Георгия и еще двоих. Борис и Дмитрий вместе решили задач столько же, сколько Василий и Евгений вместе. Дмитрий решил задач больше, чем Георгий, но меньше, чем Василий. Кто какое место занял? Запишите первые буквы их имён в порядке убывания числа решенных задач (например, АГДБЕВ)

Ответ:

11. Сколько существует таких натуральных чисел N, для которых ровно одно из чисел N и N + 973 трёхзначное?

Ответ:

12. Сколько существует чётных пятизначных чисел с произведением цифр 28?

Ответ:

13. Чтобы покрасить поверхность (все грани) деревянного кубика высотой 3 см нужно 730 мг краски. Сколько краски понадобится, чтобы покрасить деревянный ящик размером 3 × 6 × 7 дециметров?

Ответ:

14. На электронных часах высвечивается 12 : 00 : 08. Через какое время
впервые все цифры на табло часов окажутся разными?

ВНИМАНИЕ: если ответ содержит минуты и секунды, то ответ пишется через двоеточие - сначала минуты потом секунды. Пример: 5:10

Ответ:

15. По дороге в одном направлении шли два человека со скоростью 4
км/ч, причем второй вышел на три часа позже первого. Первый нанял встреченного всадника отвезти второму письмо и привезти ответ.
Всадник привёз письмо за 45 минут, полчаса ждал ответа (второй в это время писал письмо, а не шел, а первый продолжал идти) и потом повёз его обратно. Сколько времени потребуется всаднику на доставку ответа?

ВНИМАНИЕ: если ответ содержит минуты и секунды? то ответ пишется через двоеточие - сначала часы потом минуты. Пример: 5:10

Ответ:

16. Какие из результатов данных действий начинаются с цифры 1? Выпишите в ответ номера нужных примеров.
1)4385 + 5892; 2)763−677; 3)3711×358; 4)32592×98734;
5)74173787591475 : 356894725; 6)4651722726829701 : 235681;
7)10736528548858−962332147692; 8)329×268−268×273+56×132

ВНИМАНИЕ: номера ответов вводите через пробел. Пример: 5 10 15

Ответ:

17. Лифт в доме ездит с постоянной скоростью, а на каждом этаже, куда
вызван, стоит одинаковое время. Время поездки в лифте считается
от момента отправления с начального этажа до момента прибытия
на конечный. Петя ехал вниз с 11 этажа, на 9 этаже к нему подсел
Коля, на 6 этаже Таня, а на 3 этаже Витя. На первом этаже все
вышли. Петя ехал 54 секунды, а Таня 23 секунды. Сколько секунд
ехал Коля?

Ответ:

18. В трёх пассажирских поездах различное число мест: 265, 318, 477. Во
всех вагонах число мест одинаковое и большее 30. Сколько вагонов
в этих поездах вместе?

Ответ:

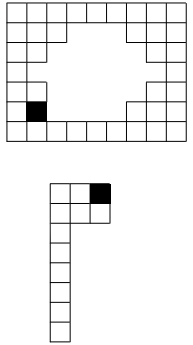
19. На рисунке изображены две клетчатые фигуры: прямоугольник 7 × 9 с дыркой и буква
P странной формы. У каждой из фигур одна клетка отмечена чёрным. Эти фигуры по
клеточкам положили на тетрадный лист так, что черные клетки находятся в точности одна над другой. Клетки фигуры и клетки листа совпадают Фигурки можно поворачивать и переворачивать. Алина посчитала, сколько клеток тетрадного листа накрыто хотя бы одной из фигурок. Какие числа она могла получить?
В ответ запишите все возможные варианты через пробел.

Для этого вопроса ответ не учитывается при подсчёте результатов

20. Расставьте в клетках фигуры числа от 2 до 11, каждое по одному разу, так, чтобы в любой полоске из трех клеток (горизонтальной или вертикальной) сумма делилась на 3.

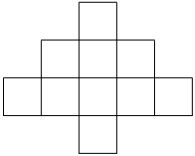
Для этого вопроса ответ не учитывается при подсчёте результатов

Приобретайте наш курс по математике!

Приобретайте наш курс по математике!

Вступительная работа по математике в 5 класс ФМЛ № 239 (Петербург). 2019 год. II вариант