Главная |
Статьи

Тест на уровень знаний
Подберите задачи для теста по своим критериям.

Вступительные экзамены в физматшколы
Вступительные экзамены в 5-й класс физматшкол Петербурга и Москвы за разные годы.
Хотите больше материалов по математике?
Курс по подготовке ребёнка к поступлению в 5-е классы престижных школ и к олимпиадной
математике.
Стоимость:
1 990 руб.
1 990 руб.
16 часов
видео
видео
Набор задач для самостоятельного решения
Видеоматериал, где подробно рассказывается, как решать задачи по следующим темам:
- Задачи на движение
- Уравнения и решение задач с помощью уравнений
- Системы уравнений и решение задач с помощью систем уравнений
- Периметр, площадь и объём фигур
- Упрощение выражений
- Множества
- Чет-нечет
- Задачи, связанные с календарём
- Свойства чисел
- Части
- Ряды
- Распилы
- Разрезание геометрических фигур
- Комбинаторика
- Взвешивание и переливание
Результаты ОГЭ как индикатор катастрофы в школьном математическом образовании
Около половины девятиклассников, сдающих ОГЭ (основной государственный экзамен) по математике, из года в год сдают его на двойки и тройки, при том, что задания там элементарные. Это катастрофа и с этим надо что-то делать.
В апреле 2020 года Минобразования разрешило регионам самим устанавливать минимальные границы итоговой аттестации 9-х классов.
Стандартные нормативы, установленные Минобром, следующие. Чтобы получить за ОГЭ по математике 3, надо набрать минимум 8 баллов, из них как минимум 2 балла по разделу "Геометрия". Для четвёрки на ОГЭ надо набрать минимум 15 баллов, из них как минимум 2 балла по геометрии. Ну для пятёрки надо набрать минимум 22 балла, из них всё те же как минимум 2 балла должны быть по геометрии.
При этом регионы могут повысить или понизить эти нормативы. Повышать их ни один регион не стал, а вот несколько регионов снизили на один балл планку, необходимую для получения тройки - с 8 баллов до 7 - потому что в предыдущие годы было слишком много двоечников.
То есть проблема решается не путём улучшения качества образования, а путём снижения требований.
Вот конкретная статистика.
В 2019 году в Омской области ОГЭ по математике сдали на двойку 11.8% учеников, а на тройку - 42.5%. То есть 54.3% сдали на двойки и тройки - то есть правильно решили меньше двух задач по геометрии и меньше 13 задач по алгебре. В Липецкой области за тот же 2019 год за ОГЭ по математике на двойку сдали 2.33% учеников, а на тройку - 40.25%. То есть 42.58% сдали на двойки и тройки. 22% девятиклассников, сдававших ОГЭ по математике в 2022 году во Владимирской области, получили неудовлетворительную оценку и будут направлены на пересдачу.
В июне 2021 г. в паблике ВК "Подслушано у учителей" учителя из разных регионов России делились результатами ОГЭ по математике в своих школах. Результаты по ОГЭ во многих местах печальные - 29 двоек из 75, 28 двоек из 4-х классов, 26 двоек из 104 и т.д.
В 2021 году в Ханты-Мансийском автономном округе четверть девятиклассников не смогли сдать ОГЭ по математике. В Красноярском крае в 2019 г. ОГЭ на двойку сдали 4.39% учеников, на тройку - 27.09%, итого в сумме - 31.48%, в 2021 г. результаты уже были намного хуже - 10.78% и 50.25% соответственно, итого в сумме 61.03%.
То, что выше указаны конкретные регионы, это не значит, что проблемы по математике только в них, а в других регионах всё хорошо. Просто мы не хотели быть голословными, и привели информацию, подтверждённую статьями на новостных сайтах. При желании таких ссылок можно было бы дать значительно больше, но нет смысла загромождать ими эту статью.
И это при том, что на весь экзамен с очень несложными (как вы увидите ниже) задачами школьникам даётся 3 часа 55 минут. И это при том, что очень многие родители специально нанимают репетиторов своим детям, чтобы они сдали ЕГЭ хотя бы на три (для кого-то и три уже хороший результат) или на 4 и 5. Хотя там задачи такого уровня, для решения которых в советской школе никому бы и в голову не пришло бы нанимать репетитора.
Рассмотрим задачи из одного из вариантов ОГЭ за 2019 г. (полностью в формате PDF вы можете скачать этот вариант здесь) и покажем, что получить 5 на этом экзамене не составляет никакого труда. По меркам советской школы большинство из этих заданий по сложности не дотягивают даже для самотоятельной работы, не то что для выпускного экзамена.
ОГЭ за 2021 и 2022 г. несколько поменялись по форме, но уровень сложности остался тем же, что и раньше. Поэтому, чтобы понять всю глубину падения математического образования в стране, можно рассмотреть и ОГЭ трёхлетней давности. А взяли мы его, потому что у нас есть статистика решения каждой из 26-ти задач в Омской области.
Вот она:


1. Найдите значение выражения: -80 + 0,3•(-10)3.
Мы помним, что троечка сверху - это значит надо умножить число само на себя три раза, и помним, как обращаться с отрицательными числами при умножении и сложении. Получаем ответ -380.
С этой задачей в 2019 г. в Омской области справились 88.66% школьников.
2. Учёный Куликов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва–Санкт-Петербург.

Путь от вокзала до университета занимает полчаса. Укажите номер самого позднего (по времени отправления) поезда, который подходит учёному Куликову.
Тут вроде любой человек, если он не идиот, сходу ответит, что правильный ответ - поезд 002А, приезжающий в 7:55. Однако, с задачей справились только 82.48% школьников. Что именно вызвало сложности у целых 17.52% учеников, которые не смогли её решить, как они в принципе что-то планируют в своей жизни, хотя бы на уровне похода в кино - решительно непонятно. А ведь 17% - это каждый шестой. То есть в 16 лет (а именно в этом возрасте дети сдают ОГЭ), каждый шестой школьник не может правильно купить билет на транспорт, чтобы оказаться в нужной точке в нужное время. И если он это не может сделать, когда ему почти каждый день приходилось решать в школе математические задачки, то как он это сможет делать в реальной жизни, где математики сильно меньше, чем в школе?
3. На координатной прямой отмечены точки А, В, C и D.
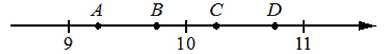
Одна из них соответствует числу
Калькулятора у нас под рукой нет, и мы в уме прикидываем, что 90:9 = 10, а 2:9 ближе к 0, чем к 1, поэтому наша точка - ближайшая к 10, которая при этом больше 10, то есть C.
С этой задачей справились 87.25% учеников.
4. Найдите значение выражения
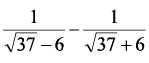
Если начать в уме приводить задачу к общему знаменателю, то станет понятно, что там будет разность квадратов: (a - b)*(a + b) = a2 - b2. a = √37, b = 6.
√372 - 62 = 37 - 36 = 1. Таким образом, уже после вычислений в уме видно, что знаменатель равен единице.
В числителе имеем (√37 + 6) - (√37 - 6) = √37 + 6 - √37 + 6 = 12.
Несмотря на "пугающий" √37, мы задачу решили в уме. Ответ - 12.
Эту задачу решили 59.35% учеников. То есть 41.65% не умеют приводить дроби к общему знаменателю, упрощать алегбраические выражения, не помнят формулу разности квадратов, и не могут (если уж не помнят формулу) просто корректно перемножить два выражения в скобках друг на друга, чтобы получить ту же самую 1, что мы получили, помня формулу разности квадратов. А ведь эти умения - база всей алгебры, которой в школьной программе уделяется много времени. Подчеркнём, что дроби - это не что-то сложное типа интегралов, это база. Это всего лишь чуть сложнее сложения и деления целых чисел. И если более 40% учеников не могут работать с дробями, то это катастрофа.
В аналитической записке, посвящённой результатам ОГЭ в Омской области в 2019 г. авторы пишут, что школьники "Допускают ошибки в применении формул сокращенного умножения; свойств степени и корня; логарифма, тригонометрии, в правилах раскрытия скобок; в разложении многочлена, квадратного трехчлена на множители; в сокращении алгебраических дробей; в нахождении числового значения алгебраического выражения."
5. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1,2 В.
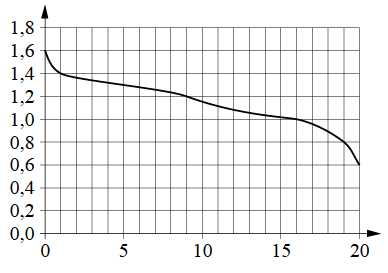
В этой задаче ничего сложного. Находим точку, где график на уровне 1.6, находим точку, где график на уровне 1.2, и смотрим, сколько клеток по горизонтали между этими точками. Получаем 9. С ней справились целых 94.35%. Остаётся, конечно, загадкой, в чём именно была сложность для тех 5.65%, кто не смог правильно посчитать клеточки на графике.
6. Решите уравнение х2 - 121 = 0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Для решения этой задачи достаточно помнить таблицу квадратов, а так же то, что при возведении в квадрат положительное и такое же отрицательное число дают одинаковый результат. Нам нужен наименьший из корней, поэтому ответ: -11. С этой задачей справились 81.7%. То, что элементарное квадратное уравнение не смогли решить аж 18.3% учеников - это, на самом деле, катастрофа.
7. Для приготовления смеси из орехов смешивают фундук и миндаль в отношении 13:12 соответственно. Сколько процентов этой смеси составляет фундук?
Задачка элементарная. Общее количество частей = 13+12 = 25. Процент, который составляет фундук - 100*(13/25) = 52%. Однако, с этой элементарнейшей задачей справились всего 67.22%. То есть каждый третий ученик не понимает, что такое проценты и как с ними работать. Непонятно, как в будущем эти дети будут решать разного рода бытовые задачи, связанные с кредитами и депозитами, например.
8. На диаграмме показано содержание питательных веществ в сливочном мороженом. Определите по диаграмме, в каких пределах находится содержание белков.
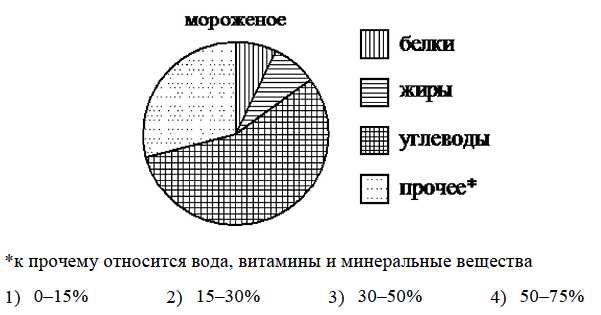
Здравый смысл нам подсказывает, что сектор белков тут самый маленький по размеру, а, значит ему соответствует наименьшее значение процентов. То есть ответ - вариант 1 (0-15%).
С этой задачей справились 89.9%. Как показывают исследования, обилие разного рода инфографики в современных СМИ всё-таки научили детей правильно эту инфографику понимать. Но и то - 10.1% всё-таки эту элементарную задачу не осилили.
9. В магазине канцтоваров продаётся 112 ручек: 17 красных, 44 зелёных, 29 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Тут тоже всё просто. Вычитаем из 112-ти ручек 17, 44 и 29 - получим 22. Это суммарное количество синих и чёрных ручек. Так как мы знаем, что их поровну, то чёрных ручек 22:2 = 11. Таким образом, суммарное количество красных и чёрных ручек - 17+11 = 28. Вероятность того, что случайно выбранная ручка будет красной или чёрной - 28/112= 0.25. Задача решается в голове, однако её смогли решить только 77.65% школьников. То есть целых 22.35% эту элементарную задачу осилить не смогли.
Кстати, занятно, что более простую задачу N7 про фундук и миндаль решило меньшее количество школьников - 67.22%. Почему эта задача N9, которая похожа на задачу N7 (ведь на самом деле, вероятность найти заданную ручку - это процент этих ручек, то есть, как и в задаче N7, всё сводится к вычислению процентов), где требуется сделать больше действий, оказалось более простой для целых 10.43% школьников (разница между 77.65% и 67.22%), требует отдельного исследования.
10. Установите соответствие между функциями и их графиками.
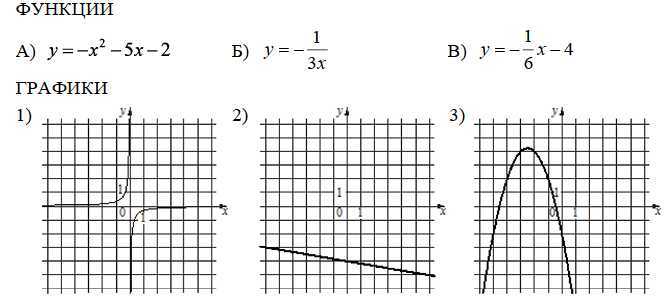
Тут много ума не надо, чтобы подставить в каждую из формулу по одному-два значений x, вычислить y, и посмотреть, на каком из графиков мы увидим соответствующее значение y.
Путём несложных вычислений получаем, что функции А соответствует график 3, функции Б - график 1, а функции В - график 2.
Эту задачу решили только 55.1% школьников. На самом деле это катастрофа. То есть почти половина учеников - 44.9%, не понимают, что такое графики функций и как с ними работать.
11. Выписаны первые три члена арифметической прогрессии: 6; 8; 10; ...
Найдите сумму первых восьми её членов.
Задача решается в уме. Шаг прогрессии - 2, значит 8-й член прогрессии - 6 + (8-1)∙2 = 20
Сумма всех членов арифметической прогрессии равна половине произведения суммы её крайних членов на количество всех её членов. То есть в нашем случае - ((6+20)∙8)/2 = 104.
Если же формула для нахождения суммы членов прогрессии забыта, то можно просто сложить все 8 членов этой прогрессии - благо, тут числа от 6 до 20, это тоже можно сделать в уме.
Эту элементарную задачу решили только 59.35%, что иначе как катастрофой назвать нельзя.
12. Найдите значение выражения
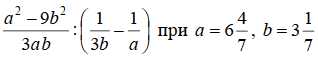
Выражение может показаться сложным только для человека, который полностью забыл, как упрощаются алгебраические выражения. Школьники занимаются этим как минимум с 5-го класса, и для них ничего сложного в этой дроби не должно быть. Если получить численный ответ в голове для этого выражения может быть сложно, то уж упростить в голове - элементарно - как минимум сходу видно, что 3ab будет сокращено, а если посмотреть на эту формулу чуть подольше, то становится понятно, что a2 - 9b2 раскладывается на (a - 3b)(a + 3b), и с учётом второго множителя, у которого в знаменателе будет (a - 3b), это самое (a - 3b) сокращается и мы получаем (a + 3b). Как мы видим, всё выражение после упрощения свелось к простому a + 3b.
Далее вместо а и b подставляем их числовые значения и вычисляем получившееся выражение с дробями, и получаем 16. Отметим, что тут даже не придётся приводить дроби к общему знаменателю, т.к. он изначально одинаковый.
Однако, эту простую задачу решили только 35.92% учеников. То есть две трети учеников не смогли её решить.
Методисты, анализирующие результаты отмечают слабое владение учащимися операций над дробями. А ведь это - база, без которой невозможно решение хоть сколько-нибудь сложных задач по алгебре.
13. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С = 6500 + 4000∙n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ дайте в рублях.
Задача в одно действие. Надо просто подставить n в формулу. Умножить 12 на 4000 легко можно в уме, прибавить 6500 тоже. Получаем ответ 54500. Однако, с этой задачей справились почему-то только 74.38% учеников. Что оказалось в ней сложного для тех 25.62%, кто осилить эту задачу не смог - решительно непонятно. Опять таки, то, что четверть учеников не могут решить задачу в одно действие, где нужно просто подставить одно число в формулу - это катастрофа всего математического образования.
14. Укажите решение системы неравенств

Это элементарная система неравенств, при решении которой главное помнить, что при делении или умножении обеих частей неравенства на отрицательное число знак меняется на противоположный. Решить эту систему вполне можно устно, проведя все преобразования в голове. Правильный ответ - вариант 1).
Эту задачу решили только 62.19%. Катастрофический результат.
Итого, в модуле "Алгбера" мы легко набрали 14 баллов, причём из 14 задач 13 решаются устно.
15. Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.
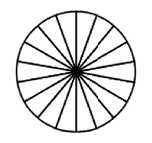
Для решения этой задачи достаточно помнить, что круг - это 360 градусов. Делим 360 на 18, получаем ответ 20. Эту задачу решили 72.78%. То есть те 27.22%, которые не смогли решить эту элементарную задачу или вообще не знали как к ней подступиться, или забыли, что круг - это 360°, или не смогли правильно разделить 360 на 18. Любая из этих причин говорит о крайне серьёзных проблемах в математическом образовании в школе.
16. В остроугольном треугольнике АВС проведена высота ВН, ∠BAC = 46°. Найдите угол АВН. Ответ дайте в градусах.
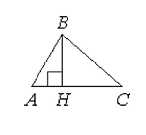
Элементарная задача, решаемая устно. Сумма углов в треугольнике - 180°. Высота - это перпендикуляр, то есть она образует с основанием угол в 90°. Таким образом, ∠ABH = 180 - 90 - 46 = 44°. Однако, эту задачу решили только 63.82% учеников.
17. Радиус окружности, вписанной в равносторонний треугольник, равен 8√3 . Найдите длину стороны этого треугольника
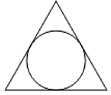
Радиус окружности, вписанной в равносторонний треугольник, высчитывается по формуле r = a/(2∙√3). Отсюда мы легко можем вычислить сторону треугольника, и квадратный корень из трёх нас не испугает, т.к. он уйдёт после перемножения сам на себя (ведь по условиям задачи радиус окружности - 8√3), и в итоге путём вычислений в уме мы получим сторону квадрата, равную 48.
Эту задачу решили 43.01%. То есть больше половины учеников не вспомнили формулу для радиуса вписанной в равносторонний треугольник окружности, и не смогли решить эту задачу другим способом, без применения этой формулы.
18. Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.
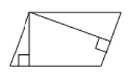
Площадь параллелограмма равна произведению основания на высоту.
48 делим на 16, получаем ответ 3. Устная задача в одно действие. Однако, её смогли решить только 80.03%. То есть почти 20% не смогли запомнить элементарной формулы для вычисления площади параллелограмма.
19. На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину её средней линии.
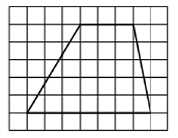
Длина средней линии равна среднему арифметическому длин её оснований. Посчитать по клеточкам длину оснований мы уж как-нибудь сможем, сложить и разделить на два тоже. Получаем ответ - (3 + 7):2 = 5. Как видим, эта задача решается устно.
Эту задачу решили 84.41%. То есть 15.59% не запомнили формулу для вычисления длины средней линии трапеции.
20. Какие из следующих утверждений верны?
1) Вписанный угол, опирающийся на диаметр окружности, прямой.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
Надо помнить, кое-что понятно из логических рассуждений (например, углы у треугольников могут быть равны, а вот длины сторон разные, значит одного равенства углов недостаточно для равенства треугольников). Верный ответ - 1.
Итого в модуле "Геометрия" мы правильно ответили на 6 вопросов, причём на все - путём вычислений в голове. Общее количество набранных нами баллов - 20, твёрдая четвёрка.
Для того, чтобы получить 5, надо набрать минимум 22 балла.
Далее в ОГЭ ещё имеется вторая часть, где есть три задачи "повышенной сложности" по алгебре и три задачи по геометрии - для тех, кто хочет получить пятёрку.
21. Решите уравнение x4 = (3x-10)2.
Извлекаем из правой и левой частей корень, получаем
x2 = |3x - 10|
В правой части у нас модуль, то есть мы имеем два квадратных уравнения
1) x2 = 3x - 10
2) x2 = -3x + 10
после переноса в левую часть
1) x2 - 3x + 10 = 0
2) x2 + 3x - 10 = 0
В первом уравнении дискриминант отрицательный, то есть корней нет, во втором уравнении корни вполне можно вычислить устно. Получим x1 = -5, x2 = 2
Эту задачу решили 12.68% учеников.
22. Баржа прошла по течению реки 80 км и, повернув обратно, прошла ещё 60 км, затратив на весь путь 10 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Элементарная задача, при решении которой надо помнить, что при движении по течению реки скорость движения баржи равна её собственной скорости + скорость течения реки, а при движении против - собственной скорости минус скорость течения реки.
Время - это путь, делённый на скорость. Суммарное время, затраченное на весь путь, состоит из двух частей - из времени движения по течению реки и времени движения против течения реки.
Таким образом, мы можем записать, что 80/(v + 5) + 60/(v - 5) = 10. Здесь v - собственная скорость баржи.
Путём несложных преобразований получим, что v = 15 км/ч.
Эту элементарную задачу из программы за 6-й класс (напомню, что мы сдаём ОГЭ за 9-й) решили только 9.77% учеников. Вот что пишут методисты из Омской области в своей аналитической записке к результатам ОГЭ за 2019 год:
Итак, мы уже набрали 22 балла, из два балла по геометрии, и тем самым обеспечили себе пятёрку по этому экзамену. Дальше решать уже необязательно, но рассмотрим ещё пару задач.
23. Постройте график функции.
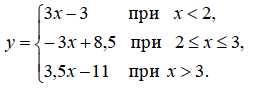
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Функция состоит из трёх участков, каждый из которых описывается линейным уравнением. После того, как мы нарисуем на графике каждый из участков, то увидим, что для определения m нам надо приравнять второе уравнение к третьему, и после несложных вычислений мы определим, что m=-0.5.
24. Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если АН = 3, АС = 27.
Элементарная задача, которой в советской школе место было бы в лучшем случае в контрольной работе, а не на выпускном экзамене.
Вот треугольник ABC с проведённой высотой AH:
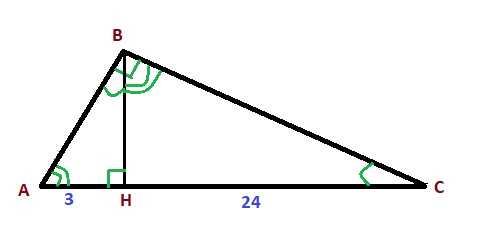
Так как AC = 27, то HC = AC - AH = 27 - 3 = 24
Общая сумма углов треугольника - 180°. Так как один угол прямой, то сумма острых углов любого прямоугольного треугольника всегда равна 180° - 90° = 90°.
Таким образом:
∠BAC = 90 - ∠BCA
∠CBH = 90 - ∠BCA
То есть ∠BAC = ∠CBH
Аналогично находим, что ∠ABH = ∠BCA
Каждый из трех углов треугольника ABC равен одному из углов треугольников ABH и BHC. В силу этого треугольники ABC, ABH и BHC называются подобными, что и есть ключ к решению этой задачи.
Нарисуем эти треугольники рядом друг с другом:

Стороны подобных треугольников пропорциональны. То есть отношения сторон при равных углах равны друг другу.
То есть в нашем случае
Значения HC и AH нам известны, поэтому:
то есть
HB2 = 24∙3 = 72
Нам даже не нужно извлекать квадратный корень, чтобы найти HB. Напомню, что задача - найти AB.
AB - это гипотенуза в треугольнике AHB (напомним, что он крайний справа на рисунке выше).
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
То есть AB2 = AH2 + HB2
AH нам известно из условия задачи, HB2 мы только что нашли.
AB2 = 32 + 72 = 9 + 72 = 81
Получаем AB = √81 = 9
Всё, задача решена. Для этого нам было достаточно вспомнить свойства подобия треугольников.
Эту несложную задачу решили 2.24% учеников.
У нас уже 24 балла, то есть мы сдали ОГЭ на пятёрку. Осталось ещё две задачки - тоже не самых сложных по меркам советской школы. Авторам лень расписывать их решение, т.к. цель данной статьи - показать, что получить 5 баллов на ОГЭ по математике при минимальных знаниях школьного курса - совсем не сложно, и для этого не нужно 4 часа времени.
25. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.
26. Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 12, а углы В и С четырёхугольника равны соответственно 115° и 95°.
Что-то странное и катастрофическое творится с нашим образованием, если такие простые задачи вызывают у наших детей колоссальные сложности. И не стоит себя утешать, что половина учеников всё-таки сдаёт на 4 и 5, так как это весьма слабые 4 и 5, которые сами по себе вовсе не свидетельствуют о хорошем знании математики (в том понятии "хорошо", как это подразумевалось в советской школе).
Очевидно, требуется основательное исследование, что стало причиной этого, и что нужно сделать, чтобы ситуацию исправить.
Стандартные нормативы, установленные Минобром, следующие. Чтобы получить за ОГЭ по математике 3, надо набрать минимум 8 баллов, из них как минимум 2 балла по разделу "Геометрия". Для четвёрки на ОГЭ надо набрать минимум 15 баллов, из них как минимум 2 балла по геометрии. Ну для пятёрки надо набрать минимум 22 балла, из них всё те же как минимум 2 балла должны быть по геометрии.
При этом регионы могут повысить или понизить эти нормативы. Повышать их ни один регион не стал, а вот несколько регионов снизили на один балл планку, необходимую для получения тройки - с 8 баллов до 7 - потому что в предыдущие годы было слишком много двоечников.
То есть проблема решается не путём улучшения качества образования, а путём снижения требований.
Вот конкретная статистика.
В 2019 году в Омской области ОГЭ по математике сдали на двойку 11.8% учеников, а на тройку - 42.5%. То есть 54.3% сдали на двойки и тройки - то есть правильно решили меньше двух задач по геометрии и меньше 13 задач по алгебре. В Липецкой области за тот же 2019 год за ОГЭ по математике на двойку сдали 2.33% учеников, а на тройку - 40.25%. То есть 42.58% сдали на двойки и тройки. 22% девятиклассников, сдававших ОГЭ по математике в 2022 году во Владимирской области, получили неудовлетворительную оценку и будут направлены на пересдачу.
В июне 2021 г. в паблике ВК "Подслушано у учителей" учителя из разных регионов России делились результатами ОГЭ по математике в своих школах. Результаты по ОГЭ во многих местах печальные - 29 двоек из 75, 28 двоек из 4-х классов, 26 двоек из 104 и т.д.
В 2021 году в Ханты-Мансийском автономном округе четверть девятиклассников не смогли сдать ОГЭ по математике. В Красноярском крае в 2019 г. ОГЭ на двойку сдали 4.39% учеников, на тройку - 27.09%, итого в сумме - 31.48%, в 2021 г. результаты уже были намного хуже - 10.78% и 50.25% соответственно, итого в сумме 61.03%.
То, что выше указаны конкретные регионы, это не значит, что проблемы по математике только в них, а в других регионах всё хорошо. Просто мы не хотели быть голословными, и привели информацию, подтверждённую статьями на новостных сайтах. При желании таких ссылок можно было бы дать значительно больше, но нет смысла загромождать ими эту статью.
И это при том, что на весь экзамен с очень несложными (как вы увидите ниже) задачами школьникам даётся 3 часа 55 минут. И это при том, что очень многие родители специально нанимают репетиторов своим детям, чтобы они сдали ЕГЭ хотя бы на три (для кого-то и три уже хороший результат) или на 4 и 5. Хотя там задачи такого уровня, для решения которых в советской школе никому бы и в голову не пришло бы нанимать репетитора.
Рассмотрим задачи из одного из вариантов ОГЭ за 2019 г. (полностью в формате PDF вы можете скачать этот вариант здесь) и покажем, что получить 5 на этом экзамене не составляет никакого труда. По меркам советской школы большинство из этих заданий по сложности не дотягивают даже для самотоятельной работы, не то что для выпускного экзамена.
ОГЭ за 2021 и 2022 г. несколько поменялись по форме, но уровень сложности остался тем же, что и раньше. Поэтому, чтобы понять всю глубину падения математического образования в стране, можно рассмотреть и ОГЭ трёхлетней давности. А взяли мы его, потому что у нас есть статистика решения каждой из 26-ти задач в Омской области.
Вот она:


Модуль "Алгебра"
1. Найдите значение выражения: -80 + 0,3•(-10)3.
Мы помним, что троечка сверху - это значит надо умножить число само на себя три раза, и помним, как обращаться с отрицательными числами при умножении и сложении. Получаем ответ -380.
С этой задачей в 2019 г. в Омской области справились 88.66% школьников.
2. Учёный Куликов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва–Санкт-Петербург.

Путь от вокзала до университета занимает полчаса. Укажите номер самого позднего (по времени отправления) поезда, который подходит учёному Куликову.
Тут вроде любой человек, если он не идиот, сходу ответит, что правильный ответ - поезд 002А, приезжающий в 7:55. Однако, с задачей справились только 82.48% школьников. Что именно вызвало сложности у целых 17.52% учеников, которые не смогли её решить, как они в принципе что-то планируют в своей жизни, хотя бы на уровне похода в кино - решительно непонятно. А ведь 17% - это каждый шестой. То есть в 16 лет (а именно в этом возрасте дети сдают ОГЭ), каждый шестой школьник не может правильно купить билет на транспорт, чтобы оказаться в нужной точке в нужное время. И если он это не может сделать, когда ему почти каждый день приходилось решать в школе математические задачки, то как он это сможет делать в реальной жизни, где математики сильно меньше, чем в школе?
3. На координатной прямой отмечены точки А, В, C и D.
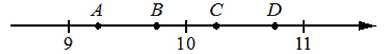
Одна из них соответствует числу
92
/
9
. Какая это точка?
Калькулятора у нас под рукой нет, и мы в уме прикидываем, что 90:9 = 10, а 2:9 ближе к 0, чем к 1, поэтому наша точка - ближайшая к 10, которая при этом больше 10, то есть C.
С этой задачей справились 87.25% учеников.
4. Найдите значение выражения
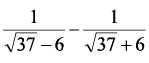
Если начать в уме приводить задачу к общему знаменателю, то станет понятно, что там будет разность квадратов: (a - b)*(a + b) = a2 - b2. a = √37, b = 6.
√372 - 62 = 37 - 36 = 1. Таким образом, уже после вычислений в уме видно, что знаменатель равен единице.
В числителе имеем (√37 + 6) - (√37 - 6) = √37 + 6 - √37 + 6 = 12.
Несмотря на "пугающий" √37, мы задачу решили в уме. Ответ - 12.
Эту задачу решили 59.35% учеников. То есть 41.65% не умеют приводить дроби к общему знаменателю, упрощать алегбраические выражения, не помнят формулу разности квадратов, и не могут (если уж не помнят формулу) просто корректно перемножить два выражения в скобках друг на друга, чтобы получить ту же самую 1, что мы получили, помня формулу разности квадратов. А ведь эти умения - база всей алгебры, которой в школьной программе уделяется много времени. Подчеркнём, что дроби - это не что-то сложное типа интегралов, это база. Это всего лишь чуть сложнее сложения и деления целых чисел. И если более 40% учеников не могут работать с дробями, то это катастрофа.
В аналитической записке, посвящённой результатам ОГЭ в Омской области в 2019 г. авторы пишут, что школьники "Допускают ошибки в применении формул сокращенного умножения; свойств степени и корня; логарифма, тригонометрии, в правилах раскрытия скобок; в разложении многочлена, квадратного трехчлена на множители; в сокращении алгебраических дробей; в нахождении числового значения алгебраического выражения."
5. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,6 В до 1,2 В.

В этой задаче ничего сложного. Находим точку, где график на уровне 1.6, находим точку, где график на уровне 1.2, и смотрим, сколько клеток по горизонтали между этими точками. Получаем 9. С ней справились целых 94.35%. Остаётся, конечно, загадкой, в чём именно была сложность для тех 5.65%, кто не смог правильно посчитать клеточки на графике.
6. Решите уравнение х2 - 121 = 0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Для решения этой задачи достаточно помнить таблицу квадратов, а так же то, что при возведении в квадрат положительное и такое же отрицательное число дают одинаковый результат. Нам нужен наименьший из корней, поэтому ответ: -11. С этой задачей справились 81.7%. То, что элементарное квадратное уравнение не смогли решить аж 18.3% учеников - это, на самом деле, катастрофа.
7. Для приготовления смеси из орехов смешивают фундук и миндаль в отношении 13:12 соответственно. Сколько процентов этой смеси составляет фундук?
Задачка элементарная. Общее количество частей = 13+12 = 25. Процент, который составляет фундук - 100*(13/25) = 52%. Однако, с этой элементарнейшей задачей справились всего 67.22%. То есть каждый третий ученик не понимает, что такое проценты и как с ними работать. Непонятно, как в будущем эти дети будут решать разного рода бытовые задачи, связанные с кредитами и депозитами, например.
8. На диаграмме показано содержание питательных веществ в сливочном мороженом. Определите по диаграмме, в каких пределах находится содержание белков.

Здравый смысл нам подсказывает, что сектор белков тут самый маленький по размеру, а, значит ему соответствует наименьшее значение процентов. То есть ответ - вариант 1 (0-15%).
С этой задачей справились 89.9%. Как показывают исследования, обилие разного рода инфографики в современных СМИ всё-таки научили детей правильно эту инфографику понимать. Но и то - 10.1% всё-таки эту элементарную задачу не осилили.
9. В магазине канцтоваров продаётся 112 ручек: 17 красных, 44 зелёных, 29 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Тут тоже всё просто. Вычитаем из 112-ти ручек 17, 44 и 29 - получим 22. Это суммарное количество синих и чёрных ручек. Так как мы знаем, что их поровну, то чёрных ручек 22:2 = 11. Таким образом, суммарное количество красных и чёрных ручек - 17+11 = 28. Вероятность того, что случайно выбранная ручка будет красной или чёрной - 28/112= 0.25. Задача решается в голове, однако её смогли решить только 77.65% школьников. То есть целых 22.35% эту элементарную задачу осилить не смогли.
Кстати, занятно, что более простую задачу N7 про фундук и миндаль решило меньшее количество школьников - 67.22%. Почему эта задача N9, которая похожа на задачу N7 (ведь на самом деле, вероятность найти заданную ручку - это процент этих ручек, то есть, как и в задаче N7, всё сводится к вычислению процентов), где требуется сделать больше действий, оказалось более простой для целых 10.43% школьников (разница между 77.65% и 67.22%), требует отдельного исследования.
10. Установите соответствие между функциями и их графиками.

Тут много ума не надо, чтобы подставить в каждую из формулу по одному-два значений x, вычислить y, и посмотреть, на каком из графиков мы увидим соответствующее значение y.
Путём несложных вычислений получаем, что функции А соответствует график 3, функции Б - график 1, а функции В - график 2.
Эту задачу решили только 55.1% школьников. На самом деле это катастрофа. То есть почти половина учеников - 44.9%, не понимают, что такое графики функций и как с ними работать.
11. Выписаны первые три члена арифметической прогрессии: 6; 8; 10; ...
Найдите сумму первых восьми её членов.
Задача решается в уме. Шаг прогрессии - 2, значит 8-й член прогрессии - 6 + (8-1)∙2 = 20
Сумма всех членов арифметической прогрессии равна половине произведения суммы её крайних членов на количество всех её членов. То есть в нашем случае - ((6+20)∙8)/2 = 104.
Если же формула для нахождения суммы членов прогрессии забыта, то можно просто сложить все 8 членов этой прогрессии - благо, тут числа от 6 до 20, это тоже можно сделать в уме.
Эту элементарную задачу решили только 59.35%, что иначе как катастрофой назвать нельзя.
12. Найдите значение выражения
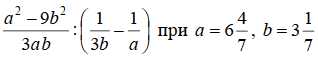
Выражение может показаться сложным только для человека, который полностью забыл, как упрощаются алгебраические выражения. Школьники занимаются этим как минимум с 5-го класса, и для них ничего сложного в этой дроби не должно быть. Если получить численный ответ в голове для этого выражения может быть сложно, то уж упростить в голове - элементарно - как минимум сходу видно, что 3ab будет сокращено, а если посмотреть на эту формулу чуть подольше, то становится понятно, что a2 - 9b2 раскладывается на (a - 3b)(a + 3b), и с учётом второго множителя, у которого в знаменателе будет (a - 3b), это самое (a - 3b) сокращается и мы получаем (a + 3b). Как мы видим, всё выражение после упрощения свелось к простому a + 3b.
Далее вместо а и b подставляем их числовые значения и вычисляем получившееся выражение с дробями, и получаем 16. Отметим, что тут даже не придётся приводить дроби к общему знаменателю, т.к. он изначально одинаковый.
Однако, эту простую задачу решили только 35.92% учеников. То есть две трети учеников не смогли её решить.
Методисты, анализирующие результаты отмечают слабое владение учащимися операций над дробями. А ведь это - база, без которой невозможно решение хоть сколько-нибудь сложных задач по алгебре.
13. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С = 6500 + 4000∙n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ дайте в рублях.
Задача в одно действие. Надо просто подставить n в формулу. Умножить 12 на 4000 легко можно в уме, прибавить 6500 тоже. Получаем ответ 54500. Однако, с этой задачей справились почему-то только 74.38% учеников. Что оказалось в ней сложного для тех 25.62%, кто осилить эту задачу не смог - решительно непонятно. Опять таки, то, что четверть учеников не могут решить задачу в одно действие, где нужно просто подставить одно число в формулу - это катастрофа всего математического образования.
14. Укажите решение системы неравенств

Это элементарная система неравенств, при решении которой главное помнить, что при делении или умножении обеих частей неравенства на отрицательное число знак меняется на противоположный. Решить эту систему вполне можно устно, проведя все преобразования в голове. Правильный ответ - вариант 1).
Эту задачу решили только 62.19%. Катастрофический результат.
Итого, в модуле "Алгбера" мы легко набрали 14 баллов, причём из 14 задач 13 решаются устно.
Модуль "Геометрия"
15. Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.

Для решения этой задачи достаточно помнить, что круг - это 360 градусов. Делим 360 на 18, получаем ответ 20. Эту задачу решили 72.78%. То есть те 27.22%, которые не смогли решить эту элементарную задачу или вообще не знали как к ней подступиться, или забыли, что круг - это 360°, или не смогли правильно разделить 360 на 18. Любая из этих причин говорит о крайне серьёзных проблемах в математическом образовании в школе.
16. В остроугольном треугольнике АВС проведена высота ВН, ∠BAC = 46°. Найдите угол АВН. Ответ дайте в градусах.

Элементарная задача, решаемая устно. Сумма углов в треугольнике - 180°. Высота - это перпендикуляр, то есть она образует с основанием угол в 90°. Таким образом, ∠ABH = 180 - 90 - 46 = 44°. Однако, эту задачу решили только 63.82% учеников.
17. Радиус окружности, вписанной в равносторонний треугольник, равен 8√3 . Найдите длину стороны этого треугольника

Радиус окружности, вписанной в равносторонний треугольник, высчитывается по формуле r = a/(2∙√3). Отсюда мы легко можем вычислить сторону треугольника, и квадратный корень из трёх нас не испугает, т.к. он уйдёт после перемножения сам на себя (ведь по условиям задачи радиус окружности - 8√3), и в итоге путём вычислений в уме мы получим сторону квадрата, равную 48.
Эту задачу решили 43.01%. То есть больше половины учеников не вспомнили формулу для радиуса вписанной в равносторонний треугольник окружности, и не смогли решить эту задачу другим способом, без применения этой формулы.
18. Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту.

Площадь параллелограмма равна произведению основания на высоту.
48 делим на 16, получаем ответ 3. Устная задача в одно действие. Однако, её смогли решить только 80.03%. То есть почти 20% не смогли запомнить элементарной формулы для вычисления площади параллелограмма.
19. На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите длину её средней линии.

Длина средней линии равна среднему арифметическому длин её оснований. Посчитать по клеточкам длину оснований мы уж как-нибудь сможем, сложить и разделить на два тоже. Получаем ответ - (3 + 7):2 = 5. Как видим, эта задача решается устно.
Эту задачу решили 84.41%. То есть 15.59% не запомнили формулу для вычисления длины средней линии трапеции.
20. Какие из следующих утверждений верны?
1) Вписанный угол, опирающийся на диаметр окружности, прямой.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
Надо помнить, кое-что понятно из логических рассуждений (например, углы у треугольников могут быть равны, а вот длины сторон разные, значит одного равенства углов недостаточно для равенства треугольников). Верный ответ - 1.
Итого в модуле "Геометрия" мы правильно ответили на 6 вопросов, причём на все - путём вычислений в голове. Общее количество набранных нами баллов - 20, твёрдая четвёрка.
Для того, чтобы получить 5, надо набрать минимум 22 балла.
Далее в ОГЭ ещё имеется вторая часть, где есть три задачи "повышенной сложности" по алгебре и три задачи по геометрии - для тех, кто хочет получить пятёрку.
21. Решите уравнение x4 = (3x-10)2.
Извлекаем из правой и левой частей корень, получаем
x2 = |3x - 10|
В правой части у нас модуль, то есть мы имеем два квадратных уравнения
1) x2 = 3x - 10
2) x2 = -3x + 10
после переноса в левую часть
1) x2 - 3x + 10 = 0
2) x2 + 3x - 10 = 0
В первом уравнении дискриминант отрицательный, то есть корней нет, во втором уравнении корни вполне можно вычислить устно. Получим x1 = -5, x2 = 2
Эту задачу решили 12.68% учеников.
22. Баржа прошла по течению реки 80 км и, повернув обратно, прошла ещё 60 км, затратив на весь путь 10 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Элементарная задача, при решении которой надо помнить, что при движении по течению реки скорость движения баржи равна её собственной скорости + скорость течения реки, а при движении против - собственной скорости минус скорость течения реки.
Время - это путь, делённый на скорость. Суммарное время, затраченное на весь путь, состоит из двух частей - из времени движения по течению реки и времени движения против течения реки.
Таким образом, мы можем записать, что 80/(v + 5) + 60/(v - 5) = 10. Здесь v - собственная скорость баржи.
Путём несложных преобразований получим, что v = 15 км/ч.
Эту элементарную задачу из программы за 6-й класс (напомню, что мы сдаём ОГЭ за 9-й) решили только 9.77% учеников. Вот что пишут методисты из Омской области в своей аналитической записке к результатам ОГЭ за 2019 год:
Единичные работы, в которых было представлено решение данного задания, не содержали первого этапа работы с задачей – составление математической модели. Решение предложенной задачи сводилось к составлению и решению дробно-рационального уравнения. Между тем при составлении модели обучающимися были допущены ошибки, свидетельствующие о непонимании описываемого процесса и связи величин, характеризующих данный процесс: при вычитании из меньшей величины большей, получали положительное числовое значение.
Можно констатировать, что и формальное выполнение алгоритма решения дробно-рационального уравнения реализовано многими обучающимися не в полном объеме. А именно, отсутствовал существенный шаг решения – нахождение области допустимых значений уравнения или отбор найденных корней через их проверку подстановкой в исходное уравнение, что вело к неверному ответу, так как среди найденных корней один являлся посторонним.
Итак, мы уже набрали 22 балла, из два балла по геометрии, и тем самым обеспечили себе пятёрку по этому экзамену. Дальше решать уже необязательно, но рассмотрим ещё пару задач.
23. Постройте график функции.
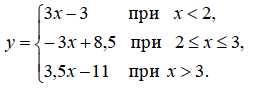
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Функция состоит из трёх участков, каждый из которых описывается линейным уравнением. После того, как мы нарисуем на графике каждый из участков, то увидим, что для определения m нам надо приравнять второе уравнение к третьему, и после несложных вычислений мы определим, что m=-0.5.
24. Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если АН = 3, АС = 27.
Элементарная задача, которой в советской школе место было бы в лучшем случае в контрольной работе, а не на выпускном экзамене.
Вот треугольник ABC с проведённой высотой AH:

Так как AC = 27, то HC = AC - AH = 27 - 3 = 24
Общая сумма углов треугольника - 180°. Так как один угол прямой, то сумма острых углов любого прямоугольного треугольника всегда равна 180° - 90° = 90°.
Таким образом:
∠BAC = 90 - ∠BCA
∠CBH = 90 - ∠BCA
То есть ∠BAC = ∠CBH
Аналогично находим, что ∠ABH = ∠BCA
Каждый из трех углов треугольника ABC равен одному из углов треугольников ABH и BHC. В силу этого треугольники ABC, ABH и BHC называются подобными, что и есть ключ к решению этой задачи.
Нарисуем эти треугольники рядом друг с другом:

Стороны подобных треугольников пропорциональны. То есть отношения сторон при равных углах равны друг другу.
То есть в нашем случае
HC
/
HB
=
HB
/
AH
Значения HC и AH нам известны, поэтому:
24
/
HB
=
HB
/
3
то есть
HB2 = 24∙3 = 72
Нам даже не нужно извлекать квадратный корень, чтобы найти HB. Напомню, что задача - найти AB.
AB - это гипотенуза в треугольнике AHB (напомним, что он крайний справа на рисунке выше).
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
То есть AB2 = AH2 + HB2
AH нам известно из условия задачи, HB2 мы только что нашли.
AB2 = 32 + 72 = 9 + 72 = 81
Получаем AB = √81 = 9
Всё, задача решена. Для этого нам было достаточно вспомнить свойства подобия треугольников.
Эту несложную задачу решили 2.24% учеников.
У нас уже 24 балла, то есть мы сдали ОГЭ на пятёрку. Осталось ещё две задачки - тоже не самых сложных по меркам советской школы. Авторам лень расписывать их решение, т.к. цель данной статьи - показать, что получить 5 баллов на ОГЭ по математике при минимальных знаниях школьного курса - совсем не сложно, и для этого не нужно 4 часа времени.
25. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.
26. Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 12, а углы В и С четырёхугольника равны соответственно 115° и 95°.
Что-то странное и катастрофическое творится с нашим образованием, если такие простые задачи вызывают у наших детей колоссальные сложности. И не стоит себя утешать, что половина учеников всё-таки сдаёт на 4 и 5, так как это весьма слабые 4 и 5, которые сами по себе вовсе не свидетельствуют о хорошем знании математики (в том понятии "хорошо", как это подразумевалось в советской школе).
Очевидно, требуется основательное исследование, что стало причиной этого, и что нужно сделать, чтобы ситуацию исправить.
Дата публикации